Device for flying a coin／１円玉飛ばし装置の原理と実験

目　次

１．適用
　本書は「コイン飛ばし装置」に適用する。

２．目的
　「コイン飛ばし装置」の原理を物理学的な見地から電磁気学、力学、電気工学を中心に解説し、計算により実験結果を予測する。次に実験装置を設計、製作して、データを計測し、予測した値と比較する。
　このレポートのテーマは、エネルギーが大きく３つの形態を経て変換されていく過程について検討し、理論から予測された値が実験で検証され、その正しさが証明されることを示し、更に、その原理の理解を深めること、を目的とするものである。

３．概要
　私が本レポートを書くきっかけとなったのは、インターネット上で偶然見かけた「コイン飛ばし装置」のホームページであった。それはどのようなものかというと、主に渦巻状に製作したコイルと高電圧発生＋充放電回路から構成され、前者にコインを載せて放電スイッチを押すとコインが上に向かって飛ばされる、という仕組みである。

　大変興味深いテーマではあるが、残念なことに、どのホームページも似たような内容である。それらは、実験装置をどうにか作って１円玉などを飛ばす写真や動画と見かけの結果を載せているだけであり、原理の説明もあまりいただけるものではない。また高校の授業で利用した例もあるが、高校の物理レベルなら、もう一歩踏み込んで、習得したエネルギーの計算の意味を理解することも可能ではないか、と思ったりもする。
　どうも今ひとつ腑に落ちないのは、いづれもその目的や理論的な根拠があやふやなままで、興味本位でやってみただけという点にあるからだろう。

　実は、簡単そうなこの実験には見落としてはならない重要なポイントがある。
　それはエネルギーの変化の過程である。

　目的には“大きく３つ”と書いておいたが、次のエネルギー遷移図に示すとおり、この実験では、正確にはエネルギーが４段階に変化していく。
　つまり、コンデンサの充電による電気エネルギー、放電によるコイルの磁気エネルギー、その電磁誘導により渦電流が発生し、更に渦電流により発生する磁気エネルギー、これらが反発して生じるコインの力学的エネルギーである。
　物質的に言えば、
　　電池　→　コンデンサ　→　コイル　→　コイン
の流れであり、図式化すると図３．１の通りである。


　
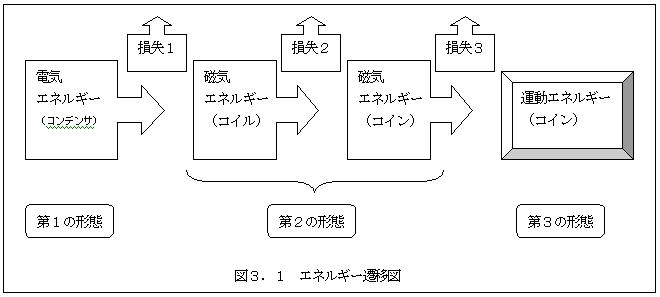
　このエネルギーの３態変化に着目し、順番に各項目を理解しなければ、この実験の意味を理解したことにはならないことに留意すべきであろう。この内の最初と最後のエネルギーは高校レベルでも計算できるものなのである。
　だが、重要な点が高校レベルでは教えられない。図の中に記載した損失に関する考え方である。