7.これまで続けてきた方針は、
一方の素子が他方の素子により影響されるその作用が
2つの素子によって占有される空間の積に比例する
という仮説を基本にしてきた。
4節で既に述べたように、仮説というものは、
それがお互いに漠然と近くに配置された素子の相互作用の問題である場合には
もはや認められない。
なぜなら、それは
その素子の大きさとそれらの相互の距離の間の関係を定めるか、
またこれらの素子にある形式を定めるかの、
どちらかが必要だからである。
これまでに見いだした、
ある素子から別の素子へと移る電気の可変量を表わす式(♂)は、
結果として、この仮説に左右されないという利点をもつ。
というのは、
ある確定的な場合に、積mm’の代わりに何が置かれても、
この特性は単に伝導力(=導電率)χに帰するので、
式(♂)は常に変わらないからである。
例として、4節で述べたように、
もしFが寸法(容積)や両素子間の平均距離といった具体的な変数に相応する関数を表わすなら、
式 αmm’(u’−u)dt は、明らかに F(u‘−u)dt に変化するだけでなく、
式 χ=dmm’s(◎) も χ=F・s に変化する。
それ故に、この方程式からFの値をとり、前述の式の中にそれを置けば、
常に
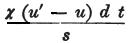
を得る。
(訳注)χ=dmm’s を変形すると、dmm’
=χ/s となり、これを αmm’(u’−u)dt に代入すると、χ(u’−u)dt/s となる。
ここで、伝導力(=導電率)χ、2つの素子EとE’の検電力の差:u’−u、中心を結ぶ距離sである。
その上、上述の検電力が各部分の全ての場所に存在するとき、
式(♂)が微粒子−その寸法はもはや漠然と小さくはない−に、
まだ有効であり続けるという事実は、ある重要性をもつ。
ゆえに、いかにこの考え方が本質的に微分学の精神につながっているか、は明白である。
というのは、
全ての場所において一様であるという、(微分)計算時の特性は、
微分学によって要求される、当然1つの要素として認められるべき、まさに独自の性質であるからだ。
もし、さらに深く、
ラプラスに始まるこの手順とここまで進めてきたこの手順との比較を始めるならば、
ある興味深い類似点に達するだろう。
例えば、無限小の距離にある無限小の質量の場合、
必然的に、有限な距離にある有限な質量の場合と同様に
(この2つの質量はともに)同じ重さを持たねばならないという全く特殊な関係がある、
ということを考慮するならば、
不朽のラプラスの理論が
−あたかも素子が互いに有限の距離に配置されているかのごとく、常に取り扱われねばならない、ということに従うと−
それにもかかわらず、どうして誤った結果をもたらすのか、直接的に明らかではない。
しかし、それが表す以上に、実際別な方法で作用することをより綿密な調査で見いだすだろう。
事実、素子の周辺のもの全てによりその変化を決定するとき、
ラプラス(の式)は、
距離の(影響)力がより小さい場合と比べると、
それが大きければ大きいほどその力を消失させるので、
そこで直ちに、かれは、無限に小さくなるその作用の違いを、事実上、微分学の精神で仮定するが、
かれはそれを有限と呼び、またそのようにも取り扱う。
そこから、彼が事実、無限に小さい距離で、無限に小さいそれを有限として取り扱う
ということが直ちに明らかになる。
しかしながら、
この表現方法に伴う重要な確実性と明瞭性を無視することで、
まだなにか言うべきことがもっとあるのかもしれない。
そして、おそらくは、ラプラスの表現手法に対し、
この点でこの考え方の利益となるように、ある正当性をもって(言うならば)、
即ち、前者は、与えられた物体の素子に関して考えられる性質について、
最低限の説明もできないばかりか、
物体の物理的な性質がまったく見失われたまま、空間の素子を想像で説明するはずである。
実例によってこの主張を解り易くするため、
等質の素子でのみ構成された自然の中の物体を何の疑いもなく想像してよい。
だが、ある方向に向けられたお互いのその位置は
別の方向に向いている時よりも異なるにちがいない。
つまり、この表現方法がすぐに示すように、
そのような物体は、ある方向に、別の方向とは異なった方法で電気を伝えるはずである。
それにもかかわらず、それらは一様で等価な密度を表わすだろう。
そのような場合に、もしそれが起きたとすると、
ラプラスに従えば、
相変わらず一般的な手順とは全く相容れない考え方に逃げこまねばならない。
一方、物体が電気を伝える方法は、
それらの内部構造を判断可能にする方法を教えてくれる。
だが、問題へのほぼ完全な無知から、それが直ちに示されることは無い。
最後に、以下のことを追加したい。
即ち、分子の作用の方法を明らかにしてきた、これまでの考え方が、
かれ(ラプラス)の熱の理論において、
ラプラスとフーリエによって進められた2つの考え方を
この考え方の中で結合し、さらに互いにそれらを調和させる、ということを。