5.これまで、それらの間に電気的な状態の均一化が生じる、素子の相互距離の影響に
注意を払わなかった。
なぜなら、今までのところは、
常に相対的な距離が変わらない素子だけを考えてきたからだ。
しかし、今や、
この交換が隣接する素子間のみに直接的に生じるのかどうか、
それとも、それがもっと離れた相手へも及ぶのかどうか、
そして、どちらか一方の仮説で、いかにして、その(変化の)大きさがその距離により変えられるのか?という問題が生じる。
ラプラスの例によると、
相手と離された2つの素子間の直接の相互作用が、有限の距離でもまだ生じる
ということに従うなら、
特殊な表現方法を使用することは、
ほんのわずかな距離で分子の作用が働き始める場合には
通例のことなのである。
しかしながら、その作用は急速に減少し、
いかに知覚可能な距離であろうとも、あまりに微小なために、
それはまったく一瞬のこととして考えねばならない。
なぜなら、
隣りの素子へ達するというだけの直接の作用、生み出された方程式、
その可変量−微分学の精神に反する不均一性をもつ−の微分には、
相対的に異なった大きさの個々の部分という仮定ゆえに、
ラプラスは結果としてこの仮説に至った、といえる。
にもかかわらず、互いに必要性のある微分方程式の項の間の
この明らかに避けられない不均衡が、
そのような研究には何か価値があると考える人々の注意を引きつけないのは、
非常に驚くべきことである。
それにより今後の考え方をもっと単純で簡潔にするという点で、この考え方は勝るので、
結果として、この謎を説明するため何かを追加しようという試みは、この場でより最適になるだろう。
電気の伝達については、事実として受け取るだけでよいし、
その結果、別の例を証明するための機会を得るまで、
入手した結果を他の似たような問題に転用することは困難ではないだろう。
6.特に、伝導性(率)の良さという言葉が正確に定義されることは不可欠である。
しかし、ここで、別の同じ環境下で、ある場所から別の場所へ一定の時間に運ばれ、
さらに2つの(素子の)間の距離を掛けた量に比例する大きさの量により、
2つの(素子の)位置の間の伝導エネルギーを表わすものとする。
2つの(素子の)位置が広げられたならば、
そのとき、
2つの(素子の)位置の寸法の中心を繋ぐ直線がそれらの距離である、
と理解しなければならない。
この考えを2つの電気素子EとE’に転用し、
さらに、それらの中心を結ぶ距離をs、電気の量をρとよぶなら、
それは正確に決められ、且つ一定の環境の下で、
一方の素子から他方の素子へ運ばれる。
さらに、それらの間の導電率をχとすると、
χ=ρ・s
となる。
次に、ρの意味する電気の量をより正確に決定していきたい。
4節によると、
極短時間に、一方の素子から他方(の素子)へ運ばれる電気の量は、
一定の距離では、検電力、持続時間と2つの素子の各大きさの間の差に一般的に比例する。
それゆえ、2つの素子EとE’の検電力(ポテンシャルまたは電圧)をuとu’、
またそれらが占有する空間をmとm’で表わすなら、
微小時間dtにE’からEへ運ばれる電気の量を次の式で得る。
αmm’(u’−u)dt
ここで、αは距離sに何らかの形で依存する係数を表わす。
u’−u が変化すると、この量は瞬間毎に変化する。
しかし、力u’とuが常に一定のままであると仮定するなら、
それは瞬時dtの大きさに依存するだけとなる。
その結果、単位時間へとそれを拡張する。
単位力に等価な、今の一定の力の差u−u’を定めるなら、
そのとき、それは
αmm’
となる。
電気のこの量は
同じ環境下で、位置が不変且つ一定である2つの素子EとE’のものであり、
その説明は、正に言及してきた伝導パワー(=導電率)の決定に費やされるだろう。
というのは、
単位力と等しい検電力の一定の差とともに、
単位時間におけるE‘からEへ移される電気の量をρによって理解すれば、
ρ=αmm’、それから χ=αmm’s
を得るからである。
(訳注:導電率は、χ=ρ・s で表される。)
この後の式から
αmm’(=χ/s) の値を取り出し、
次の式
αmm’(u’−u)dt
に代入すると、
直ちにE‘からEへ通過する電気の可変量に対する式
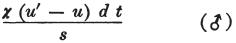
を得る。
この式は、すぐわかるように、以上で述べた微分方程式の諸項間の不調和を伴わない。