11.これを確立することで、次にこの問題をさらに前へ推し進め、
そして、第一に、同種の円筒状または角柱状の物体における電気の運動を考えたい。
そこでは、その中心線に垂直で、各断面全ての領域に渡る位置すべてが、
同時発生的に等価な検電力を有する。
ゆえに、電気の運動はその中心線の方向にのみ発生できるのである。
多数の断面により、無限小の厚さのディスク(円盤)に分割されたこの物体を考え、
それで、検電力が、そのようなディスクのペア(対)に関して、
各ディスクの全外周(円周)でほとんど変わらないならば、
6節で与えた式 ♂ は、あるディスクから別のディスクへ通過する電気の量を決定するために適用できる。
だが、これまでの節で述べてきた、無限小距離限定での作用の距離の制限により、
その性質はかなり変更されるので、
除数が無限に小さくならなければ、すぐにそれは消える。
次に、横座標の原点について、一定不変で無限にある断面の一つを選択し、
さらに、どこでもいいが、第一(の素子)から第二(の素子)までの距離をxで表わす
と仮定するなら、
dxはそこにあるディスク(円盤)の厚さを表わす。
それをMと呼ぼう。
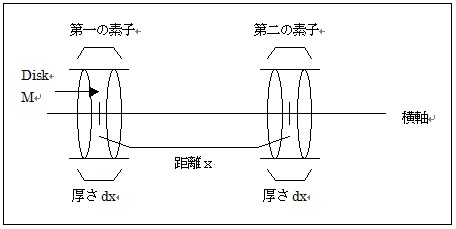
このディスクの厚さを、あらゆる場所で同じ大きさであると考え、
さらに、ディスクM内で、時間tに表れる検電力をuと呼び、その横軸をxとするなら、
結果として、一般的に、uはtとxの関数となるだろう。
その上、x+dxとx−dxがxについて個々に置き換え可能なとき、
uの値であるu’とu1を仮定すると、
u’とu1は明らかに、ディスクMの両面の隣にあるディスク(円盤)の検電力を表わす。
つまり、横軸x+dxにある一方をM’で、また、横軸x−dxにあるもう一方をM1で
表わすということである。
そして、ディスクMの中心から、ディスクM’とM1それぞれの中心への距離はdxである
ということが明々白々である。(訳注1)
その結果、6節で与えられた式(♂)により、
もしχがディスクM’とM1の伝導パワーを表わすならば、
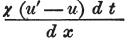
は、u’−u
が+か−かにより、
時間dt
の間にディスクM’からディスクMへ、
または後者から前者へ転送される電気の量を表わす。
同じ方法で、M1とMの間の同じ伝導パワーを認めるとき、
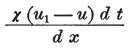
は、
式の値が+のとき、M1からMへ通過する電気の量を、
式の値が−のとき、MからM1へ通過する電気の量を表わす。
ディスクMが微小時間dtに、物体内部で電気の運動から受ける電気の量の全変化は、
結果として
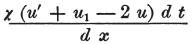
であり、
さらに、この値が+であるとき、電気の量の増加を、
また、この値が−のとき、電気の量の減少を示す。
しかし、テイラーの定理によると、
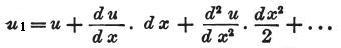
さらに、同じ方法により、
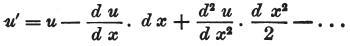
その結果、
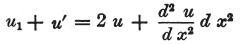
となる。(訳注2)
これによると、ディスクM内に存在する電気の量の全変化を正に発見したこの式は、
時間dtの間、
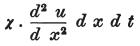
に変換される。
ここでχはあるディスクから隣接するディスクへ流れる伝導パワーを表わし、
それを均質な物体の長さ(方向)の至る所で不変であるべきものと考える。
この値χが、無限小距離の作用により
円柱状又は角柱状の物体の断面に比例するということが、
ここで観測されるはずである。
それゆえに、ωでこの面積を示し、
さらに、残りの部分もχと呼ぶことで、その値χからこの要因を分離すれば、
前者の式は次のように変わる。
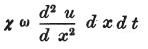
さて、ここでχは断面の大きさとは無関係な物体の導電率を表わす。
そして、相対導電率と呼ぶべき前者とは反対に、物体の絶対導電率と名付けよう。
今後、導電率という言葉がどこで無条件に現れようとも、絶対導電率として常に理解すべきである。
これまで、ディスクが隣接する大気から受ける変化を考えてこなかった。
だが、この影響は容易に決定できるかもしれない。
例えば、横軸xにあるディスクの円周をcで表わすなら、
そのとき、c・dxは大気に晒されるその表面部分となる。
その結果、9節で述べたクーロンの実験によると、
bcu・dx・dtは
瞬時dtの間に、大気中で電気が移動することにより、ディスクMに発生する
電気の変化量である。
ここで、bは大気の同時発生的性質とは独立してはいるが、同じ大気については一定の係数を表わす。
それは、uが+のとき減少を、またuが−のとき増加を表わす。
しかし、最初の仮定によると、
この作用は、物体の同じ断面において、検電力の不均一を生じることはありえない。
さもなくば、少なくともこの不均一さはほんの微量なので
感知可能な変化がもう一方の量に生じることはない。−その環境はボルタの回路でほぼ推測されるであろう。
ディスクM内の電気の量が瞬時dtに受ける全変化が