１３．これまでの２つの節で、
その長さ（の方向）または中心線に垂直な各断面の全領域にわたり、
同じ検電力がとにかく常に存在する、という仮定に立ち、
等質の角柱状物体について常に注目してきたと同時に、
そのような物体における電気の拡散を調べてきた。
次に、種類は同じだが、異なった物質で作られた２つの角柱状物体ＡとＢが隣接し、
且つ互いに共通面で接触している場合を考慮しよう。
ＡとＢともに横軸の原点に置き、
ｕでＡの検電力を、ｕ’でＢの検電力を表わすなら、
χが、常に各物体に固有の物質が示す一定の値のとき、
ｕとｕ’は共に１１節の方程式（ａ）で決定される。
- （訳注）方程式（ａ）は以下のとおり。
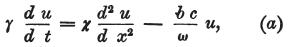
ここで、ｕはｔとｘの関数,χは導電率
ＡとＢともに横軸の原点に置き、
ｕでＡの検電力を、ｕ’でＢの検電力を表わすなら、
χが、常に各物体に固有の物質が示す一定の値のとき、
ｕとｕ’は共に１１節の方程式（ａ）で決定される。
ｕはｔとｘの関数を表わすが、横座標ｘが物体Ａ内にあるかぎり、その関係は継続する。
一方ｕ’もｔとｘの関数を表わすが、横座標ｘが物体Ｂ内にあるときのみ、その関係は継続する。
（訳注）χは導電率であり物質固有の値を示す。
- しかし、次に説明するこの共通の表面にはいくつかの他の状態もある。
- この目的のために、ｕとｕ’の個々の値を示すなら、
−まず、それらは共通面において仮定している−
１０節で発展させた法則に従うと、
これらの個々の値の間で、次の方程式
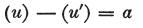
が成り立つことを見いだす。
ここで、ａは、２つの物体の性質に依存する一定の量を表わす。
この状態−それは検電力に関係する−の一方で、
第二のもの−それは電流に関係する−がまだある。
即ち、第一に、共通な表面における電流は、
２つの物体内で、等しい大きさと同じ方向を持たねばならない、
ということである。
さもなくば、もし共通因子ωを保持するなら、
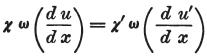
となり、χは物体Ａの、χ’は物体Ｂの実際の伝導力（＝導電率）を表わす。
さらに、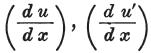
は,直接的に共通な表面で決まる
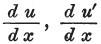の特有の値であり、
横軸の原点が共通表面にとられていなかった場合である。
この最後の方程式の必要性は容易に述べることが出来る。
つまり、２つの電流が共通表面で等価なエネルギーをもたなくとも、
もう一方の物体によりそれ（共通表面）から（電流が）持っていかれる以上に
一方の物体からこの表面へより多くの電流が伝達されるだろう、
ということである。
そして、この差が全電流の限られた部分であるなら、
検電力はまさにその場所で増加するだろう。
事実、驚くべきその電流の多さを考えると、
証明されるまで、観測に時間がかかるだろうが、
検電力は、最短時間で極度に高い値に達するだろう。
さらに、
この状況が無限の量のマイナス（−）の電気により証明されるのと同様に、
もう一方の物体に妨害されて、共通面を通過する電気量よりも
一方の物体から共通表面へ入る電気量の方が多いはずである。
接触している２つの物体が基本的に同じであるということは、
前述の決定内容の有効性を決めるにあたり、絶対的必要条件というわけではない。
これが、同じ断面のさまざまな位置で、
もし検電力が同じ断面のさまざまな位置でほぼ同じならば、
一方の角柱状物体の断面は、他方の角柱状物体のそれとは大きさや形が異なるだろう。
そして、電気が平衡しようとするこの大きなエネルギーを考慮することで、
その物体が良い伝導体であるとき、それはその事例とは異なるだろう。
そして、その（良い伝導体の）長さはもう一方の寸法をはるかに超えているのである。
この場合、全てが前と変わらず、
物体Ｂの断面は、どこであろうと、Ａのそれとは区別されねばならない。
その結果、２つの物体が接触している場所での、第二の条件付方程式は
次のように変化する。
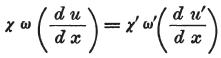
ここでωはまだＡの断面を表わすが、ω’はＢの断面であり、今は前者（Ａの断面）とは異なる。
それらは延長した物体Ａや、異なった２つの角柱状物体Ｂ、Ｃの中にも存在する。
そしてそれはＡの一方の表面上に直接、共に配置されている。
この場合、χ’ω’ｕ’が物体Ｂを、χ”ω”ｕ”が物体Ｃを表し、χωｕがＡを表すなら、
１つの条件付き方程式の代わりに、次の２つの式
（ｕ：Ａの検電力、ｕ’：Ｂの検電力、ｕ”：Ｃの検電力）
を得る。
ここでａは物体Ａ、Ｂ間の電圧を、ａ’はＡ、Ｃ間の電圧を表わす。
同じ方法で、われわれは次に、第二の条件付き方程式の代わりに次の式を得る。
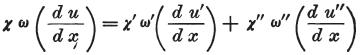
ω：円柱状又は角柱状の物体の断面
χ：ディスク間の伝導力（＝導電率）
更に多数の物体が接続された場合、
これらの方程式がどう変わらねばならないかは直ちに明らかである。
（これまで）述べてきたことは、そのような（複雑な）場合に、
この方程式を実行することでその変化を解明することが可能なので、
これらの複雑な状況の中にこれ以上立ち入らない。
１４．誤解を避けるため、これらの観測の終わりに、
もう一度正確にこの公式の普遍妥当性の範囲内で、
応用の範囲（the
circle of apprication）を説明しよう。
この全調査は、
同じ断面の全ての部分の検電力が等しく、
さらに、その断面を通ってある物体からもう一つの物体へ電気が移動するとき、
その断面の大きさが変化する場合にのみ限定される。
しかしながら、
この問題には、しばしば、これらの条件のうちどちらか一方を不要にする状況を生じるか、
さもなくば、少なくともそれらの重要性を減らす
という特徴がある。
そのような状況の知識は利用することに意味があるので、
ここに１つの例により最も目立つ点を説明しよう。
銅や亜鉛が角柱状で等断面のとき、
さらに、流体が同じく角柱状で、断面が同じかそれより小さく、その末端で金属と接触するとき、
銅や亜鉛や水のような流体の回路はすっかり以上で述べた式に収まるだろう。
いや、これらの最後の条件だけが流体について満たされるとき、
金属は等断面を有するか、またはそうでなくてもよい。
さらに、互いにそれらの断面すべてで接触しているか、さもなくば一部分でのみ接触していてもよい。
しかもそれらの形は、まったく角柱状でなくともよい。
そして、それにもかかわらず、その回路は常にわれらの公式から引き出される法則に必ず従うのである。
というのは、金属内部でかくも容易に生じる電気の運動は
そのようなかなりの範囲で、流体の非伝導性に妨害されるからである。
そして、それは、
金属の至るところで等価なエネルギーを伴い、
完全にそれ自身を拡散するための十分な時間を得て、
流体内では、われわれの計算が見出したその条件を回復する。
しかし、その角柱状流体が金属に対し、その表面の小さな部分で接触するだけの場合、
それはかなり異なった問題となる。
そこに達する電気がゆっくりと、
流体の非接触面へかなりのエネルギー損失をともなって進むだけであるため、
そこからさまざまな種類の電流と方向が結果として現れる。