ガルバーニ電気の回路における電流の力を決定するための方程式から、以前に発見されたそれ（方程式）と共に、回路の各部に、電気の力が与えられることにより、ボルタの回路に含まれるすべての現象（の原因）が容易且つ正確に、推定されるだろう。

前者（第一の方程式）は、先頃、この分野で疑問の余地のない、正確で確実な測定ができる装置による徹底した実験(編注1)　から導かれてきた。

後者（第二の方程式）はそれに関わるあらゆる観察結果を表わす。

つまり、それは最も正確な精度を持って既に大量に存在するのであり、既に発表された実験のリング（輪）には、もはや含まれないという結論を導く。

今、それらの結果に関する短い報告書により証明しようと望むかぎり、両者は、自然と協力して絶え間なく進歩する。

同時に、両方程式がその状態が永続する（編注2）　すべての可能なガルバーニ電気の回路に当てはまる、ということが認められるのは当然だろう。

その結果、それらは、特殊な場合としてボルタの電堆を含み、そのため、電堆の理論は個々の解説を必要としない。

明白にするため、私は、方程式

　　
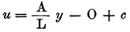
を使用する代わりに、第三の図を利用するだけであり、その結果、それから描かれる結果すべてが一般的に有用であることを単に認めるにすぎない。

次に、電気（電流）の分離は、ガルバーニの電気回路中に拡散しつつ、さまざまな場所で、恒久不変の段階的変化を維持する。

（訳注）オームがモードと呼ぶＦｉｇ．３の図のような段階的変化、つまり電位勾配を言っている。

電気（電流）の力は同一の場所では可変であるが、より厳密な点検をするのは当然である。

これが、電圧計でガルバーニ電気の回路の或る場所の作用を自由に決めることができ、さらに瞬時にそれを生じることができる、この現象の不思議な可変性の理由である。

この特質を説明するために、わたしは図３に戻りたい。

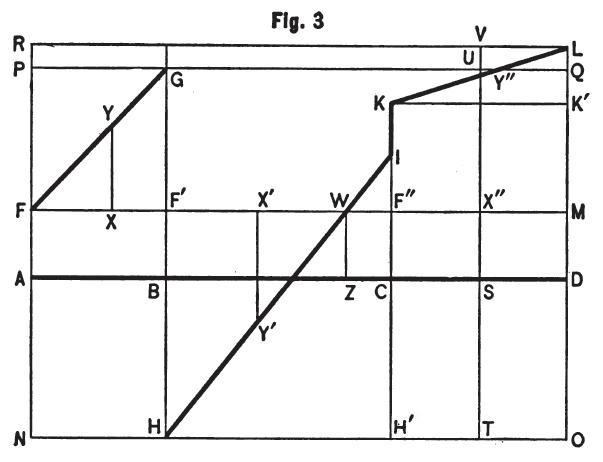
（電気の）分離の図、FG、HI、KLが、,どんな回路の性質からも、常にすべて完全に決定されるので、回路ADのその場所は、見たとおり、固有の原因に依ることなく固定されているが、縦軸の方向において、全てのその場所に共通する動きにより生みだされる何らかの変化を仮定できる。

２つの線の互いの位置により表わされる回路の各点の電気的な状態は、絶えず、そして、随意に、外的な影響により変わるだろう。

例えば、ADがいつでも回路の実際の状態を表わしている位置にあるとき、即ち、縦軸SY”はその長さによって、
そのような縦軸があるべき回路のその点での、電気（電流）の力を表わし、さらに、A点と一致する電気（電流）の力は、同時に線AFによって表現されるだろう。

もし今、A点がある方法でゼロ電位にされたなら、線ADはFMの位置に移動するだろうし、また、前からS点に存在する力は、X”Y”の長さにより表現されるだろう。

それゆえ、この力は、SX”の長さと一致するために、急な変化を受ける。

もし回路がZ点でゼロ電位にされたなら、同じ変化がおきただろう。

なぜなら、縦軸ZWはAFのそれに等しいからだ。

接触部はBC部内に作られてはいないので、もし回路が、２つの部分ABとBCが結合する点で論じられたなら、NOへ進めたADを考えるべきである。

S点の電気（電流）の力は、この場合、TY”により示される力へと増大されるだろう。

だが、もし接触部に発生するゼロ（電位）がさらに同じ場所、即ち、AB部内を除く、ABとBC部が互いに接触する場所で発生したならば、線ADはPQへ移動することになるだろう。

さらにS点にある力は、UY”により表現される負の力に落ち込むだろう。

最後に、D点をゼロ電位にするために、もしバッテリが準備されたなら、線ADをRLの位置に規定すべきだ。

さらにS点の電気の力はVY”により示される負の力を帯びるだろう。

これらの変化の法則は明らかであり、一般的には次のように表わされる。

ガルバーニ電気の回路における各点は、電気の力に外見上作用するもの、つまり、外部的な影響により、回路の他のどの点でも、直ちにもたらされる同じ変化を間接的に受ける。

ボルタの回路の各点は、ただ１点が受ける同じ変化を、ひとりでに（全てに）受けてしまうので、大量の電気（電流）の中のその変位は、全回路中に広がりながら、その一方で、すべての点の合計に比例する。

＜一部略＞

この単純な法則から、結果として次の明らかな現象が生じる。

即ち、ｕRが、物体に伝えられる電気（電流）の量であるということは明らかで、
　　（ｕ１−ｕ）・ｒ＝ｕ・Ｒ　
であり、そこから
　　
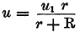
を得る。

それゆえに、物体により受ける電気（電流）の強度は、接触させる前に、回路が接触部分で持つそれ（電気の強度）に近ければ近いほど、Rはｒに対しより小さくなる。

（訳注）
ｕ＝ｕ１・ｒ／（ｒ＋Ｒ）の式から、ｒ＞＞Ｒ　または　Ｒ→０　のとき、ｕ＝u１となる。
つまり接触前後の電流値が同じになる。

それは　R＝r　のとき、半分に等しく、
さらに、Rがｒに比べて大きくなればなるほど、より小さくなるだろう。

（訳注）
ｕ＝（ｒ／ｒ＋Ｒ）・ｕ１の式から、ｒ＝Ｒのとき、ｕ＝u１／２となる。
つまり接触後の電流値が接触前の値の半分になる。

これらの変化は、領域Rとｒの相対的な大きさに依存するだけなので、回路の性質上の特徴の意味や程度には関係ない。

それらは回路の実際の質量ばかりか、回路との接続を行うことでもたらされる異質の質量(foreign masses：非導電物質)によっても決定される。

もしコンデンサの理論とこの事実を関連付けるなら、非常に驚くべきイェガー（編注1）によって言及されたコンデンサとボルタの回路のすべての関係の説明に至る。

（編注1）Schweigger’s Jahrbuch（シュバイガーの年鑑）,1826. Part2
（編注2）オームは“状態が永続する回路“への彼の法則の応用をはっきりと認めているように思える。