|
私は既に他の場所で、法則のさまざまな形式に関連する長さについて、相互にさらに取り扱った。
一般式
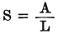
から結果として出てくるボルタの回路のきわめて多数の個々の特性から、ここで私はほんの少し言及してみたい。
熱電気回路と水電気回路、この二者の区別.
もし、電圧の合計がそれによって影響を受けないならば、部品の組み合わせにおける変化が電流の大きさには影響しない、ということは直ちに明白である。
そしてまた、電圧の合計と回路の全縮小長が同じ比率で変わるとき、電流の大きさも変わることは無い。
その結果、他の回路の電圧に比べて、電圧の合計が非常に小さい回路は、その縮小長(抵抗)の減少が電圧(起電力)の強制喪失にとって代わるとき、エネルギーという点で他の回路における電圧と等しい電流をさらに生じるかもしれない。
この条件の中に、熱電気と水電気の回路の特有の相違の原因がある。
前者では、金属のみが回路の部分として存在する。
後者では、金属の伝導力と比べると、水のような流体では伝導力が非常に小さい。
たとえ、全ての点で、それらの寸法が等しかろうと、また、少なくとも、この減少の度が過ぎない程度に、それらの実際の長さを短くすることにより、また、それらの断面を拡大することにより縮小されるとき、かなり大きくなろうとも、
流体の縮小長については、金属部分の縮小長のすべての比率とは全く異なる。
それゆえ、それは、熱回路の縮小長は、一般的に、水回路のそれよりもずっと小さい、ということであり、
その点から、
たとえ、熱回路における電流の大きさが、水回路におけるそれよりも低いわけではなくとも、
前者と同じ比率でさらに小さく電圧を推測するだろう。
同じエネルギーの電流を生じる熱回路と水回路の大きな違いは、
同じ変化が両者に生じるとき、次の根拠に示されるように明らかである。:
熱回路の縮小長がL、その電圧の合計がA、水回路の縮小長がmL、その電圧の合計がmAとしよう、
そのとき、前者の電流の大きさはA/Lによって、また後者はmA/mLで表わされる。
その結果、両回路において同じとなる。
しかし、もし縮小長として同じ新たな値λが導入されるなら、この同等性はもはや存在しない。
つまり、電流の大きさは最初は 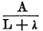 に、さらに 次は に、さらに 次は 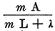 になる。 になる。
もしこの決定に、たとえ、見せかけであろうとも、m、L、λのという量の評価を関連づけるならば、
単純な水回路は、確かに熱または化学的な分解の作用をλの内に生じることができる、という場合において、
単純な熱回路は1/100も、別の場合には1/1000の必要不可欠な力の一部も占有しない可能性がある、
ということを容易に確信させられるだろう。
ゆえに、その中に同じ作用が無いことが容易に理解されるだろう。
例え、その電流の強度が、そのような影響を生み出す水回路よりも、この意味でよりいっそう増大する可能性があっても、
(例えば、それを構成する金属の断面の増大による)熱回路の縮小長の減少が、それらの影響の産物の原因ではありえない、ということも理解可能である。
金属物体と流動液体の導電率のこの違いは、おそらく正確にここで言及されるであろう水回路の場合に現れる特殊性が原因である。
通常の環境下では、流体部の縮小長は金属部のそれと比較して、非常に大きい。
即ち、後者は無視できるであろうし、さらに、前者は全回路の縮小長の代わりとなるだろう。
しかし、そのとき同じ電圧を有する回路内の電流の大きさは、流体部の縮小長に反比例する。
その結果、もしその流体部が同じ実際の長さと同じ導電率を有するそのような回路のみが比較されるなら、
そのとき、これらの回路における電流の大きさは流体部の断面に直接比例する。
しかしながら、
金属部の縮小長が、もはや流体部のそれに対して無限に小さいかのごとく見なされない場合、
−つまり、金属部が非常に長くて薄いとき、さもなくば流体部が良導体であり、巨大な終端面を持つときにはいつも、このケースが生じる−もっと複雑な定義がこの単純な定義に取って代わるにちがいない、
ということが見落とされるはずがない。
式 S=A/L から、容易に次のことを知ることができる。
それは、
一部分がボルタの回路から成り、また、別のもので置き換えられ、さらに、この変化の後、電流の強さと同じ起電力がそのまま残る場合、これらの2つの部分は同じ抵抗を有する、
ということである。
その結果、それらの実際の長さはそれらの導電率と断面の積と同じである。
それゆえに、そのような部分の実際の長さは、それらが同じ断面を持つとき、導電率と同じであり、
さらに、それらが同じ導電率を有するとき、その断面と同じである。
これらの2つの関係のうち第一のものにより、
最初に言及した過程を凌駕する進んだ方法でさまざまな物体の導電率を決定することができるのであり、
しかも、既にベクレルや私自身がさまざまな金属に対して時間を費やしてきた。(編注1)
第二の関係は、
最初にディビ−によりなされた、さらに最近は私自身(編注2)によってなされたように、
断面の形による影響とは無関係であることを実験的に証明するのに役立つかもしれない。
バッテリの起電力と抵抗は(直列の)素子の数に依存する。
ボルタの電堆では、電圧の合計と単純な回路の縮小長は、それを構成する電極(訳注:極板のこと)の数でよく表される。
[ バッテリ内で続く化学的な作用により生じる電気の全てを電流という形式で手に入れることは決してない。
手に入れた電気の総量、いいかえれば、電流の力は回路の抵抗の総計で割った起電力の総量に等しい。
かくして、Fが実際の電流の力、即ち、熱、電磁気、化学的作用、またはその他のなんらかの効果を生じるそのパワー
を意味するとしよう。
Eは起電力、Rが電線と流体の抵抗のとき
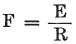
である。
この違いは、ボルタの回路で得られる電気の総量がニュルンベルグのオーム教授の数学的研究の影響による。
さらに、実験的にダニエル、ホイートストーンなどにより立証された彼の式は、これまで発見されてきた電流の力に関わるた全ての調査研究の基礎と見なされるだろう。
ボルタの電池の電極数の増加により、さらに電気を増大することができるが、同時に、回路の流体部により生じる抵抗の量も増大する。
この両方の場合に備えるべく、回路が適切な導体−丈夫な銅線のような−により完成されれば、両方の場合に同じ結果を得る。
起電力と抵抗が同じ量で増大される、
つまり、
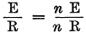
である。
Electricity Noad,
revised by
preece pp198、199.]
それゆえに、もし、1つの回路における全電圧の総量をA、縮小長をL、バッテリの電極数をnで表わすと、
閉じたバッテリ回路の電流の大きさは明らかに 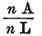 であり、 であり、
一方、ただ1つの閉じた回路では、 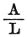 である。 である。
(編注1)一般物理会報, 5月,1825,and
シュバイガー年鑑, 1826,Part2.
(編注2)ギルバートのアナーレン、nn, Folge, 11巻
,253ページ , and シュバイガー年鑑 1827
|