２３．瞬間的には、恒久的な状態（安定状態）にならない場合、
それは、いつも乾電池内で（起きる）ため、
その期間の回路の変化に対し、完全な方程式
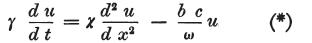
から始めるべきである。
なぜなら、この場合、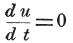
を検討できないからであり、
さらに、項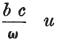
はその（方程式（＊）の）中に残ったままか、
さもなくば、それ（方程式（＊））から消去しなければならない。
ただし、検討時に、その回路が大気の影響を受けると考えるか、それともそうでないかによる。
ここで再び、
前の節から、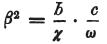
、さらに
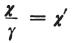とおくと
前の方程式は次のように変化する。
そして、直ちにβ＝０を認めることで、
大気の影響が方程式に残らないことを知るのである。
今の事例では、
ｕは、ｘとｔの関数であることを表わすが、
時間ｔが増加するにつれて、次第に時間ｔに依存しなくなり、
ついには、単なるｘの関数となる。
そして、それは、周知の性質を伴った、その回路の恒久的状態を表わす。
この後者の関数をｕ’とし、ｕ＝ｕ’＋ｖと置くと、ｖは明らかにｘとｔの関数である。
すると、それは、回路が恒久的状態（安定状態）から逸脱することを表わし、
その結果、一定時間の経過の後、完全に消える。
次に、方程式（＊）において、ｕの代わりにｕ’＋ｖを代入し、
さらに、ｕ’がｔと独立であり、
また、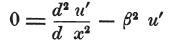
という性質であることを念頭におけば、
方程式
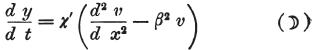
は、そのとき、関数ｖの決定に関して変わることはなく、
方程式（＊）と同じ形式をまだ持っているが、
ｖがｕとは異なった性質のｘとｔの関数であり、そのため、その最終決定は大いに簡単になる
という点でそれとは異なる。
最初にラプラスにより得られた形式の方程式の積分は、
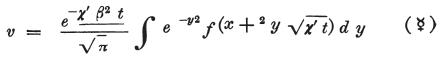
である。
ここで、
ｅは自然対数の底を、πは円周と円の直径の比を、
ｆは個々の問題に特有な性質から決定される任意の関数を表わす。
一方、積分の範囲はｙ＝−∞からｙ＝＋∞まで取らねばならない。
ここでｔ＝０のときｖ＝ｆｘとなる。
なぜならその範囲では、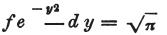
となるからである。
これより、ｆ＝０の場合の関数ｖを求める方法がわかれば、
同様にｆｘを求めることができ、その結果、任意の関数ｆを求めることができるはずである。
次に、一般的には ｖ＝ｕ−ｕ’ であるが、
時間ｔを瞬時と見なすなら、
回路の両端に接触することにより、電圧が発生し、
ｔ＝０のとき、ｕは明らかにこれらの両端でのみ値が決定され、
回路の他の場所全てで、ｕ＝０となる。
したがって、回路の全領域で一般的にｔ＝０のとき、ｖ＝−ｕ’である。
さらに同時に回路の両端でのみ、ｖ＝ｕ−ｕ’となる。
それ故に、
回路が、最初からそれ自身と完全に接触したままであったと考えるなら、
常にその両端でｖ＝０であり、
それゆえに、ｔ＝０のとき、回路の内部でｖ＝−ｕ’、その端ではｖ＝０となる。
これまでの調査によると、
ｕ’は、回路の各場所において既知のものとして見なされ、
同様にｔ＝０のとき、これはｖにも適用される。
そのとき、ｘが回路内の１箇所にある限り、任意の関数ｆｘの形式を知ることができる。
しかしながら、ｖの決定のために行われたこの積分は
ｘの＋と−全ての値における関数ｆｘの知識を必要とする。
かくして、
熱の拡散に関する研究により広まった、
回路の領域についての関数ｆｘの知識を前提とする、前述の方程式のためのそのような形式を持つ
その変換が知られることとなった。
２ℓが回路長を表わし、横軸の原点がその中心に置かれるとき、
この変換がそれに適用可能となる。
即ち、
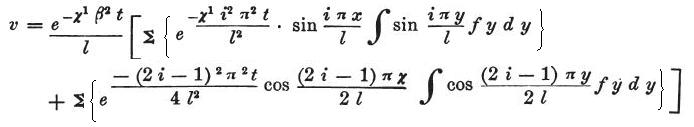
となる。
ここで、総和はｉ＝１からｉ＝∞までとられ、積分はｙ＝−ℓ からｙ＝+ℓ までとる必要がある。
次に、この方程式で、ｆｘの代わりに値−ｕ’を代入すると、
これまでの節で述べた仮定に従い、ａが接触場所の電圧を表わすなら
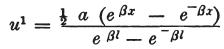
となり、さらに示された範囲を積分すると、
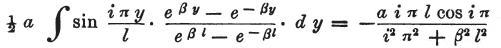
を得る。
そして、
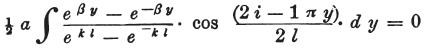
となる。
ｖの決定のため、方程式は
となり、最後に、ｕ＝ｕ’＋ｖなので
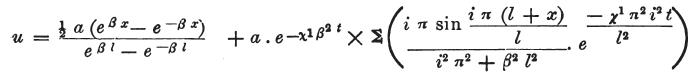
となる。
この方程式で、例えば、β＝０、つまり大気の影響を考慮に入れないとき、
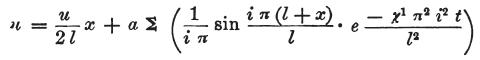
となる。
ｕの決定のために発見された方程式において、
右から第二項の値が時間の増加につれてどんどん小さくなり、
ついには完全に消えてしまう
ということが容易に認められる。
この回路の恒久的な状態（安定状態）がそのとき生じたのである。
この瞬間は、式の形式から明らかなように、
減少した伝導力（＝導電率）により、また、増大した回路の長さにより、
もっと大きな度合いで妨げられる。
しかしながら、ｕについて見出したこの式は、
仮定した回路が、何らかの外的な妨害によりその本来の状態を変えられないかぎり、
完全に保たれる。
この回路が、いつでも（どこかの場所で、推論上の接触により、瞬時に生じる）外的要因により
恒久的状態（安定状態）に強いて変更されるなら、
前述の方法は、別の場合に生じようとする何かの変化を受けるにちがいない。
（一部略）
そこで、乾電池の、また一般的には非常に長い回路の特殊な現象が探索され、
（そして、バッセ、エルマン、アルディーニの実験で使われた膨大な長さの回路は、このクラスに属する。）
さらに、後者（長い回路）の場合に規定されるべきである。
即ち、それらの膨大な長さによる影響が
伝導性の改善や面積の拡大により、除去されることはない、
ということである。
Ｃ．電流という現象
２４．１２節で進めた内容に従い、
電流の大きさは、角柱状物体では一般的に、その場所ごとに次の方程式により表現されるだろう。
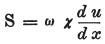
ここでＳは電流の強度を意味し、
ｕは、横座標上のｘにある回路のその場所における検電力、
一方、ωは角柱状物体の断面を表わし
χは同じ場所におけるその伝導力（＝導電率）を表わす。
いくつかの部分から構成された回路について
１８節で見出した一般式とこの方程式を関連づけるため、
次のように表わすことができる。
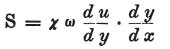
さらに、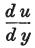
の代わりに、その一般式から生じる値
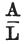を代入し、
さらに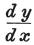
のかわりに、同じ節から容易に推定できる
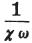を代入する。
その値は２つの励起点の間にある各場所について有効であり、
そのとき、非常に簡単な方程式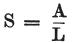
を得る。
ここでＬは回路の全抵抗を意味し、Ａは起電力の全合計である。
［ 基本方程式は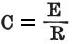
または
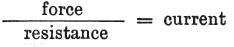である。
３つの要素Ｅ，Ｒ，Ｃの内いづれか２つが分かれば、第三の値を次のように計算できる。
電流．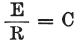
ここで、力（検電力＝電圧）と抵抗は既知である。
起電力は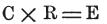
である。
ここで、電流と抵抗は既知である。
抵抗は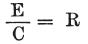
である。
このように、既知の起電力（ボルト）を電流（アンペア）で割ることにより
回路の全抵抗が得られる。
電気学．シュプレーグ．第一版，１８７５．１９９，２００ページ ］
この方程式により、
多くの角柱状部分から構成されるボルタの回路の電流の強度を得る。
そして、それは恒久的状態（安定状態）をもたらし、
周囲の大気の影響を受けず、
さらに、全ての場所で同じ検電力を有する１つの断面の影響を受けない。
この範疇には、良く起こる事例が含まれているので、
最も注意深い方法でこの結果を分析できるだろう。
Ａが回路内の全電圧の総和を表わし、
またＬが全ての個々の部分の縮小長（抵抗）を表わすことから、
そこで、第一に、
発見した方程式からボルタの回路の電流に関する次の一般的な特性を結果として得る。
Ａ．電流は、ボルタの回路の全ての場所で強度が等しいこと
また、定数ｃの値とは関係ないことは明白である。
即ち、これまで見てきた通り、
限定された場所では、検電力の強度が決まっているからである。
開いた回路では、電流は完全に停止し、
この場合、縮小長Ｌは無限に大きな値となる。
（訳注）
開いた回路とは、電池に回路が接続されていない場合である。そのときの電流Sはゼロとなる。
オームの公式
で、S=０となるのは、縮小長L＝∞のときか、電圧A＝０の場合である。
確かに、数学的には上の２つの条件が成り立つが、今日では、開いた回路には電圧が印加されていないし、物体の抵抗値（L）は変化しないのであるから、後者の方に意味があるといえる。
だが、当時、ボルタの電池の電圧は不安定であったため、このような解釈、つまり回路の縮小長を変化させるという解釈になったと思われる。
したがって、次に述べられている“全電圧の総和とその全縮小長は、全く変化しないか同一比である”という言葉に、電圧と抵抗が固定値であるとは断定できない当時の理由が表れている。
Ｂ．その全電圧の総和とその全縮小長が、全く変化しないか同一比であるとき、
ボルタの回路における電流の強度はそのまま変化することはない。
だが、縮小長（L）が変わず、電圧の総和（A）が増大するにつれて、
逆に、電圧の総和（A）は変わらず、回路の縮小長（L）が減少するにつれて
それ（S：電流の強度）は増大する。
この一般的な法則から、われわれは特に次の結論を引き出せる。
（１）全電圧の総和が変わらないとき、
回路を構成する一部分を入れ換えることで、個々の励起点の配列と分布に相違があったとしても、
電流の強度に影響しない。
したがって、例えば、銅、銀、導線、亜鉛と流体の順に構成された回路で、
銀と導線の互いの場所を変えても、電流が変化することはない。
なぜなら、
金属について既に述べた電圧の法則に従い、
この置き換えは、事実、個々の電圧を変えることはあっても、その総和を変えることはないからだ。
（２）たとえ、回路の一部分が取り去られて、他の角柱状の伝導体をその場所に入れ替えたとしても、
ボルタの電流の強度は変わらない。
ただし、両者が同じ縮小長を持ち、
どちらの場合も、電圧の総和が同じでなければならない。
またその逆も真である。
別の角柱状の伝導体とその部分の１箇所を入れ替えても、
回路の電流が変わらず、
さらに、電圧の総和が変わらないことが確認できるとき、
入れ替えられた２つの伝導体の縮小長は同じである。
［ “等質の伝導体の事例におけるこれらの研究結果は、一般に‘オームの法則’と呼ばれる。
オームの法則
１つの回路のある部分の両端に作用する起電力は、電流の強度と回路のその部分の抵抗の産物である。
ここで、新たな言葉、伝導体の抵抗−それは起電力とそれが生じる電流の強さの比で定義される−が採用される。
オームが、実際の物理量に一致するということを実験的に行って示さなかったなら
この言葉を採用しても、非科学的な値であっただろう。
即ち、伝導体の性質が変わるときのみ、それが有限な値を示すということである。
第一に、それゆえ、伝導体の抵抗は、それを通って流れる電流の強度とは無関係である。
第二に、その抵抗は、伝導体が保持する電気的なポテンシャルと、伝導体の表面の電気の分布密度とも無関係である。
それは
伝導体を構成する材料の性質、その部分の集合体の状態やその温度に
完全に依存する。
伝導体の抵抗は、１万分の１、または１０万分の１以内の値で計測されるだろう。
さらに、非常に多くの伝導体が検査され、
オームの法則の正しさへの、われわれの確信は今や非常に高い。”
電気磁気学．マクスウェル．１８７３．第一巻．２９６，２９７ページ ］
（３）常に同数の部品と同じ物質で構成され、
さらに、個々の電圧が変化しないと終端まで見なされ、
同じ順序で（部品が）配列されたガルバーニ回路を考えるなら、
この回路の電流は、
その部品の長さが変わらないなら、その部分全ての断面が増大するのと同じ割合で増加し、
さらに、断面が変わらないなら、その部分全ての長さが一様に減少するのと同じ割合で増加する。
（訳注）オームは、最後の２行で抵抗が断面積に反比例し、長さに比例することを述べている。
これは、彼が確実に R
∝ ℓ／A を意識していることを意味している。
回路の一部分の縮小長が他の部分のそれをはるかに超えたとき、
電流の強度は主にこの部分の寸法に依存する。
さらに、例えば、この一部分だけに注目するなら、
ここで発表された法則が非常に簡単な形式になるのは当然のことだろう。
Ｂ．（２）で達したこの結果は、
さまざまな物体の導電率の決定に便利な道具を提供する。
例えば、長さが ℓ とℓ’、断面積がωとω’、伝導力（＝導電率）がχとχ’
の２つの角柱状物体を考えるなら、
それらが既に述べた回路の部分を代わりに構成するとき、
両物体はボルタの回路の電流を同じ強さで保持するという特性をもつ。
さらに、両者は変化しない回路の個々の電圧を保ち、
そのとき、
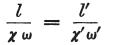
となり、その結果、
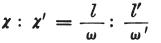
となる。
それゆえに、
両物体の伝導力（＝導電率）は直接的にそれらの長さに比例し、
それらの断面に反比例する。
（訳注）Ｐ208（３）で、既にオームは、抵抗が断面積に反比例し、長さに比例することを述べているにもかかわらず、伝導力（χ：導電率）についても同じ性質であるとしている。
オームは電流Ｓと導電率χは比例関係にあるとＰ203で定義しているので、それが電流の流れやすさを意味すると確信しているはずである。したがって、ここは誤植か単なる記述ミスであると思われる。
今日の導電率（ρ：電気伝導度）は電流の流れやすさを意味し、Ｓ／ｍ（ジーメンス／メートル）で表わす。
ジーメンスは抵抗の逆数１／Ωである。（抵抗は電流の流れにくさ、導電率は電流の流れやすさである。）
さまざまな物体の伝導力（＝導電率）の決定に、この関係を使う場合、
また、実験のために同じ断面の角柱状物体
−それは、事実、精度のために不可欠である−を選択するなら、
それらの長さにより、その導電率を正確に測定できるだろう。