|
27.反対に、ΛがLより大きいとき、
ボルタの(電池の)組合せから、最も大きな出力が得られる。
さらに、実際のところ、
ΛがLより4倍大きいときは、2つの電極で、
また、ΛがLより9倍大きいときは、3つの電極で、以下同様に、
構成される場合が最良である。
回路に同じ強度の電流が流れていることは、電流が磁針に影響を与えるのと同じく、電流により回路の外部の作用が増大することを示している。
(訳注:以下はコイルの作用についての話である。)
明快にするため、次のように仮定しよう。
磁針への電流の作用を試験するため、
回路の一部が一定の半径の円で構成され、
さらに、磁針の回転の中心が磁気子午線上に配置されている。
(訳注)磁気子午線:地磁気の北と南を通る大円。北極と南極を通る真子午線とはズレがある。
正確に数回巻かれた特殊なコイルは、
個々のコイルに同じ電流が流れることにより、磁針に強力な影響を与えるだろう。
ゆえに、コイルの並びがお互いに近すぎるからといって、
たとえ、コイルの間に非伝導性物質を重ねて、(コイル同士を)分離したとしても、
それらはまだ、互いに非常に近いので、磁針に対する互いの位置はまったく変わらないと見なされる、
と考えるなら、
それらは、増加したコイルの数に比例する、より大きな影響を針に与えるだろう。
そのようなアレンジメントは倍率器と呼ばれる。
では、Aがある回路の電圧の総和、Lがその縮小長であるとしよう。
さらに、Λもn回巻きの倍率器(複数巻きコイル)で作られた、嵌入伝導体の縮小長であるとしよう。
そのとき、1回巻きの(コイル)の縮小長をλで表わすなら、Λ=nλとなり、
磁針への倍率器(複数巻きコイル)の作用は値 
に比例するだろう。
しかし、その回路の1つのコイルの作用は、倍率器(複数巻きコイル)でないとき、
同じ基準値 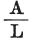 に従う。
そして、そのコイルが同様に作られているということから、
回路のその部分は、
倍率器(複数巻きコイル)内と同様の性質を持つはずである
と考えられる。
そして、そのコイルが同様に作られているということから、
回路のその部分は、
倍率器(複数巻きコイル)内と同様の性質を持つはずである
と考えられる。よって、前者と現在の作用の差は

である。
ここで、nLが 
より多いか少ないかにより、+または−になる。
結果として、
磁針への作用は、
n巻きのコイルで作られた倍率器により増大または減少させられるだろうし、
嵌入伝導体無しの回路の縮小長のn倍が、
嵌入伝導体伝導体ありの回路の全縮小長より大きいか小さいかによる、
ということになる。
nλがLとは比較できないほど大きいなら、磁針への増幅器の作用は 
となるだろう。
この値−倍率器(ガルバノメータ)による動作の極限を指示する−については、
その強弱に関わらず、さまざまな注目すべき特性をもっている。
さらに言及するなら、
この倍率器は非常に多くのコイルで作られており、
その作用の大きさは、ほぼ間違いなく、(倍率器の)限界値に等しいと考えられる、
と理解できる。
この回路におけるコイルの作用が 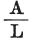 であるため、
倍率器の作用は、同じ回路については、 
である。
この2つの作用は、縮小長λとL同様に、お互いに同じ比である。
それゆえに、
この2つの作用と2つの縮小長のうちの一方を知れば、他方を知ることができ、
さらに同じ方法で、
2つの作用の内の1つが、もう一方の作用と2つの縮小長から調べられるのである。
倍率器の動作限界が 
であるため、
λが変わらないとき、
回路における電圧Aの総和が減少するのと同じ比率で、それ(倍率器の動作限界)は小さくなる。
それゆえ、
さまざまな回路における同じ倍率器の極端な動作を比較することにより、
それらの相対的な電圧を決定できるだろう。
同時に、
いくつかの単一回路がボルタの(電池の)組合せで作られ、
さらに、実際に、電極の数と直接比例関係にあるとき、
倍率器の極端な作用が増大する、
ということが理解できる。
(一部略)
倍率器のコイルの実際の長さを ℓ、導電率χ、断面ωとすると、
そのとき、 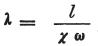
であり、その結果、倍率器の極端な作用は

となる。
そこから、
同じ回路において、等しい直径のコイルからなる2つの倍率器の極端な作用は
それらの導電率と断面の積に比例する、といえる。
それゆえ、これらの極端な作用は、2つの倍率器の中で起きている。
その違いは、
これらの金属の導電率に比例し、それぞれ異なった金属で作られている、
ということだけである。
そして、倍率器が1つの金属による同じ渦巻き(コイル)で作られているとき、
それらの極端な作用はその断面に比例するが、
磁針への回路の部分の作用は、他の似たような環境下でも、電流の大きさに比例する、
という基本的な仮定からすべて決定される。
ずっと以前から、直接的な実験がこの仮説の正しさを認めてきたのである。
28.次に、同時に存在する複合的な伝導率を考えたい。
例えば、1つの開いた回路を考える。
その両端はさまざまな伝導体に接続され、並列に接続されているとする。
電流はどのような法則により隣の伝導体に拡散するのだろうか?
この質問に答える場合、
11〜13節の考え方から直接進めるのがいいだろう。
しかし、
25節で確認したボルタの回路の特性から、要求された目的をより簡単に達成できるはずだ。
簡略化のため、
回路の開放により消滅する前者の電圧はないか、
挿入された伝導体により生じる新たな電圧も無い、
と仮定しよう。
つまり、
λ、λ’、λ”などが、開いた回路の両端に接続された伝導体の縮小長を表わし、
さらに、その回路の両端の検電力の差をαとすると、
伝導体が挿入された後、
上記の差が隣接する伝導体の端でも生じる、いうことである。
その後、この仮定によれば、この伝導体によりもたらされる新たな電圧は無い。
次に、13節によると、
この回路の電流の大きさは、並列の伝導体の全電流の総和に等しくなければならない。
伝導体が並列になっているということは、
回路を多くの部分に分割して考えればよい。
このとき、25節によると、
各隣接する伝導体の、また回路の類似の部分の電流の強度は、それぞれ

(λ、λ’、λ”:伝導体の縮小長、α:回路の両端での検電力の差)
である。
これより、第一に、
それぞれに分けられた伝導体の電流強度はその縮小長に反比例する、
という結果を得る。
次に、
回路内の全ての並列の伝導体を同じ特性の単一の伝導体に置き換えて考えると、
そこの電流はそのまま変化しない。
そのとき、第一に、
25節によると、αが同じ値のままでなければならない。
その上、この伝導体の縮小長をΛとすると、
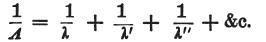
でなければならない。
これまでの説明から、次のことが結論できる。
Aが全電圧の総和を、Lが、隣接または並列の伝導体無しの回路の全縮小長を表わすとする。
伝導体がその回路に直列に接続している時、
その電流強度は、

で表わされる。
また、縮小長がλの伝導体が接合された時、
その電流強度は、
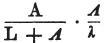
で表わされる。
また、縮小長がλ’の伝導体が接合された時、
その電流強度は、

で表わされる。
縮小長がλ”
の伝導体が接合された時、
その電流強度は、
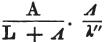
で表わされる。
以下同様。
ここでΛについては、方程式
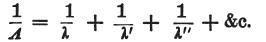
から得られるその値により決定するはずである。
|