Fluid Mechanics／オイラーとコーヒーカップの渦

図１：コーヒーかき混ぜ中。見事な渦です。

図２：ＲＭＦ・ステラー

１．身近な現象−コ−ヒーカップの渦−を考える

 スプーンでカップ内のコーヒーをかき混ぜたときや洗濯機内に渦が発生することは、多くの人が経験を持っていることと思います。（図１）

今回はコーヒーと人手の代わりに、ＲＭＦ・ステラー（図２）により非接触でカップ内の水に回転運動を与え、この写真を記録し実寸を測定します。

その一方で、力学的解析（質点の運動）による運動方程式と回転流体の運動方程式（圧縮なし、渦無し）を立て、水の表面（自由表面）の方程式を求めます。

最後は記録した写真と方程式による曲線の関係を比較し、自然現象を運動方程式がどの程度記述できるのかを調べてみます。

２．解析的な方法を試してみる

　２．１．一般式を求めよう

力学的解析から回転する液体の自由表面上にあるｍ[g]の質点を考えます。

この質点は中心からの距離x[m]の同じ周上を速度ｖ[m/s]で回転運動しているものとします。（図１参照）

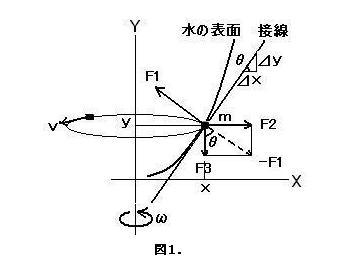
Ｆ１：ｍが水表面から受ける力（抗力）

Ｆ２：遠心力（逆方向は向心力）　ｍ・ｖ^２／x

（x：回転中心からの距離 ）

Ｆ３：ｍに働く重力　（ｇ＝9.8［m／s^２］）

　質点の運動はＦ１、Ｆ２、Ｆ３の３つの力のバランスの上に成り立ちます。つまりｍは同じ位置を回転し続けるものとします。

　　接線の傾き　　　　(極限） 　 　　　①

　　力のつり合い　   　　　　　 ②

が導かれます。よって①＝②より

　　　　          ③

　が求まります。

　見慣れた常微分方程式です。解が何かは既に想像可能ですね。

２．２．微分方程式を解こう

次に角速度をω[rad/s]とすると、周速度はｖ＝ω・ｘで表わされます。これを代入し積分すると

　　　      ④

（初期条件：ｘ＝０、ｙ＝０より積分定数＝０）

　となり、ついに解を求めることができました。

　④は確かに解なのですが、ω[rad/s]と実験で得られる測定値との関係はどう考えればよいでしょうか？

回転数の単位は１分間の回転数［min^−１］ですが、回転角［rad］との関係を考えてみます。

（［rpm］は正式な単位としては現在使われません）

　１分間の回転数をNとすると、１秒間あたりＮ／６０回転、これに２πをかければ［rad］に変換できることがわかります。よって、

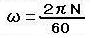
が得られます。これを③式に代入すると、

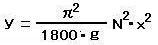
が得られ、更にｇ＝９．８［m/s²］を代入すると

　　（有効数字２桁）　　　⑤

となり、これでようやく測定可能な数値、回転数と回転半径を入れて計算できる式になりました。

　図２．５に回転数２００、３００、４００、５００[min^-1]毎に算出した方程式⑤のグラフとデータを示します。

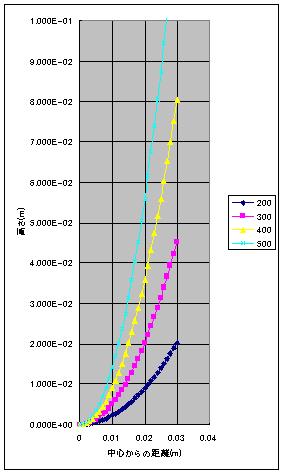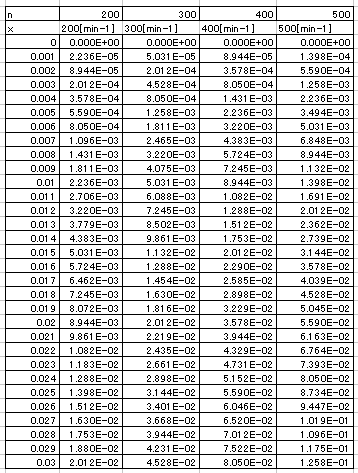
　　　　　　　　　　　　　　　　図２．５

　ＲＭＦ・ステラーで回転数を設定し、回転数300,400,500[min-¹]時の写真を撮ります。図３．６に示します。水の高さや幅などの寸法もメモしておきましょう。200回転は渦が小さいため省略。

　　　　　　　　　　　　　　　図２．６

　図３．７は、グラフ（図３．５）と回転する水（図３．６）を原寸（１ｃｍ単位）にあわせて重ね合わせたものです。

　製作にあたり、フリーソフト［普通のものさし Version 1.5.2］を使用させていただきました。

　　　　　　　　　　　　　　図２．７

　現実は３次元ですから、方程式⑤をｙ軸の周りに回転した曲面が水の表面（自由表面）になるわけです。

　ここで３次元ソフトがあると面白いのですが・・・

さて、曲線は極小点からある程度の半径まで水の自由表面に良く近似していますが、カップの縁に近づくと大きなずれを生じます。

何故でしょうか？

この力学的解析では、自由表面の運動を半径ｘで等速回転する質点（剛体）の回転運動と仮定しました。

よって運動方程式③が立てられた時点で、ｙとｘの関係がある放物線の形

ｙ＝ｃ・ｘ^２（ｃは定数）になっていることが見て取れます。

従って、コップの縁に近づくほど実際の水の表面とは合わなくなるのは当然と言えます。

では、より正確な方程式を立てるにはどうしたらよいでしょうか？

　それは流体力学（ オイラーの方程式 ）のお世話になることにほかなりません。

  では、次の解析へ・・・

と、その前にご精読いただきありがとうございました。

コーヒーでも飲んで一息入れましょう。