音楽家がオクターブと呼ぶ和音はあまりにも明らかに耳を打つので、わずかなずれも容易に知覚できるということを、殿下はこれまでにお気ずきになられたことと思います。
このようにFの鍵盤を弾くことで
１オクターブ高いｆの鍵盤は、聴覚のみの判断により容易にそれに調子を合わせられる。
もしこの音を発生するはずの弦が少しでも高すぎるかまたは低すぎると、
聴覚はすぐに過ちを犯してしまう。
そして、完全に調子の合った２つの鍵盤を押すこと以上に簡単なことはない。
このように、われわれは歌う場合に音声がちょうど１オクターブ高いか低いかの
一つの音からもう一つの音へ滑らかに移動することに気が付く。
しかし、F音からｄ音へ直ちに移るよう要求されたら、
例えば、普通の歌手ならば楽器の手助けが無いかぎり、
容易に間違ってしまうかもしれない。
F音に固定した場合、すぐにｄ音へ移行することはほぼ不可能である。
その上、F音をｆ音に調和させることは非常に容易であり、
そしてF音をｄ音に調和することは非常に難しい、
この相違の理由は何か？
その理由は既に行われた観察から明らかである。
それはこういうことである、
即ち、F音とｆ音は１オクターブの違いが有り、
さらにｆ音の振動数は正確にF音の２倍である。
この和音を認識するためには、あなたは１対２の比率のみを考慮しさえすればよい。
つまりそれは、私が以前に用いた点の表現によりすぐに目に印象付けたように、
同じ方法で耳に影響を与える。
そのとき、比率が簡単であるか、
小さな数で表現されればされるほど、
より明確に知識が姿を現し満足の感情をもたらすということを、
あなたは容易に理解するだろう。
その上、設計者らは慎重にこの主義（行動原理）に仕えている。
かれらは事情が許す限り、簡単にかれらの仕事でそろって比率を使用する。
この知識は明らかでありがたいので、
彼らは通常、ドアや窓の高さを横幅の２倍にし、
至る所で小さな数で表現可能な比率を使用する。
同じことが音楽でもうまく適用できる。
理性が音と音との間に存在する関係を認める限りにおいてのみ、和音は気に入られる。
そして、それは小さな数で表現できるので、この関係はよりいっそう容易に理解可能なのである。
では、ユニゾンにおける２つの音の意味する同等の関係に続いて、
２対１の比率はおそらくもっとも単純であり、
これこそが１オクターブの和音を備えているのである。
それ故に、この和音があらゆる他のコンソナンス（協和音）以上に多くの長所を持つことは、
明らかである。
このように、和音または音楽家により命名される２つの音の間隔を説明することにより、
直前の音よりも１以上オクターブが高いＦ、ｆ、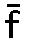
、
、
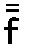のような
さまざまな音を考えてみよう。
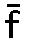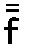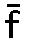ｆからF、からｆ、から、から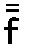の間隔が１オクターブなので、
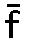からFの間隔は２オクターブ、
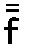からFの間隔は３オクターブ、
からFの間隔は４オクターブである。
さて、F音が１回振動する間に、ｆ音は２回振動し、
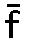音は４回振動し、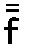は８回振動し、は１６回振動する。
それ故に、1オクターブは１：２の比に一致し、
２オクターブは１：４の比、３オクターブは１：８の比、
４オクターブは１：１６の比でなければならない。
そして、１：４の比は１：２の比ほどには簡単ではない、
というのはそれ（１：４の比）はそれほど目立たないので、
２オクターブは１オクターブのように容易に耳で知覚できない。
まして３オクターブは知覚できず、４オクターブでは全く知覚不可能である。
それ故に、ハープシコードの調律で、
あなたがF音に調整するとき、
単純なｆのように２オクターブの・に調律することは容易ではない。
まして、中間のオクターブを経て音を上げずに、
３オクターブの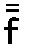や４オクターブのに調律することはより困難である。
同様に、これらの和音はコンソナンス（協和音）という用語で理解される。
そして、ユニゾン（同音）のそれがもっとも単純であるように、それらは次の段階に従い変化するのである。
１度、ユニゾン、１：１の比率で示される
２度、隣接するオクターブ、１：２の比率
３度、２倍のオクターブ、１：４の比率
４度、３倍のオクターブ、１：８の比率
５度、４倍のオクターブ、１：１６の比率
６度、５倍のオクターブ、１：３２の比率
など、音が知覚可能な限りのもの。
そのようなものが、われわれがこれまで案内してきた知識、
コンソナンス（協和音）と呼ばれる和音である。
しかし、これまでのところ、われわれはコンソナンス（協和音）の他種について、
まして音楽において使われるディソナンス（不協和音）について何も知らない。
私がこれらの説明を続ける前に、
私は、２倍振動を含む音がもう一つの音に含まれるという、
２つの音の間隔を与えるオクターブという名前に関する一つの所見を追加する必要がある。
あなたがオクターブC、D、E、F、G、A、B、ｃにたどり着く前に、
７度上げるハープシコードのプリンシパルストップ時
（principal stops：オルガンの主要音栓の閉鎖）のその理由をあなたは理解する。
Cを最初に数えるとｃは８番目であるからである。
そして、この分割は次の手紙で説明される性質の一定の連続する音の間隔に依存する。
１７６０年５月３日