|
5.地球上の緯度経度を得る方法
科学技術の進んだ現代では、地球上の2地点PとQ間の距離は容易に取得できます。
1つは、WEB上でグーグルサービスを利用するものです。これを使えば、日本列島上のどこであっても、地図を拡大しつつ十字カーソルに合わせるだけでQ点を定めることができます。その緯度経度は常に度分秒で表示されるという優れものです。
http://user.numazu-ct.ac.jp/?tsato/webmap/sphere/coordinates/
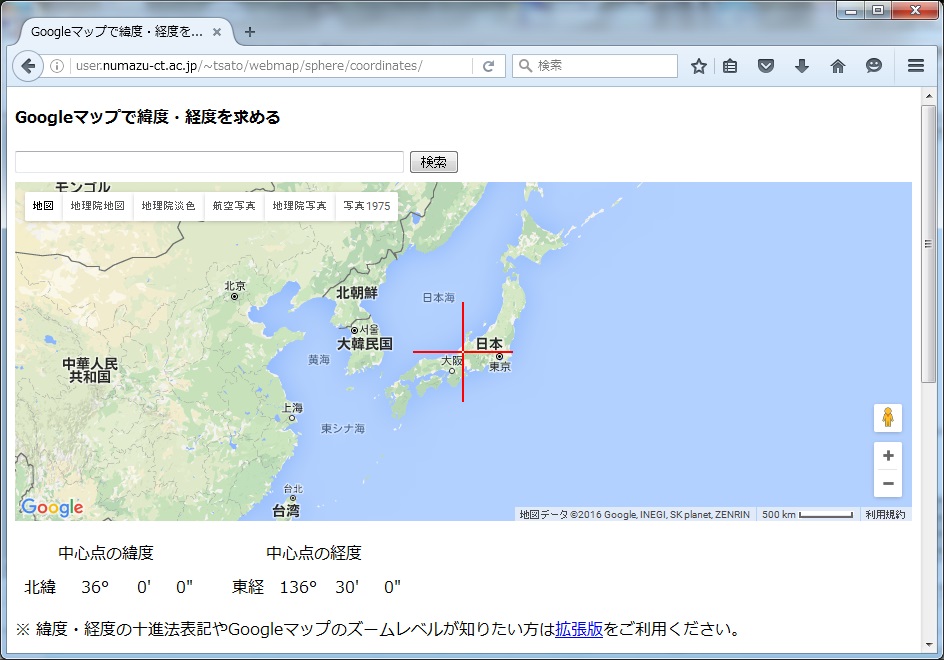
図5.1 グーグルマップによる緯度経度の取得
これによりP点の緯度経度も確定します。(経度はP、Qともに同じ。)
2つ目は、EXCELファイルにマクロを埋め込んだフリーウェア「excelgmap」です。それは住所と名称を記入して取得ボタンをクリックするだけで、その場所の緯度経度がセルに表示されるというものです。
(パスワードで保護ざれていないため、小数データから度分秒への変換やPQ間の距離計算式などを記述でき大変便利です。)
他にもいくつかありますが、以上の2つが使いやすかったので例に挙げました。
6.地球上の2点間の距離−ヒュベニの公式
わたしたちは、自分たちが生活している狭い範囲では定規や巻尺を使ったり、少々離れた所では測量機器(レーザー使用)を利用して2点間の距離を容易に測ることができます。
それらは直線距離を測るための道具ですが、一体どの位の距離まで測ることができるのでしょうか?
砂漠やサバンナで生活する人々は、われわれには確認できないような距離であっても何かがやって来るのが見えるといいますが、やはり人間の視力には自ずと限界がありますし、地上には起伏もあり測定時の障害となります。そこで、海上において(ジオイド面でもよいですが、)視力の限界を遥かに超えた距離まで計測できるレーダーを使用した場合を考えてみます。
例えば、海上で
互いに2mの高さからレーダーで測定した場合、探知距離は、
公式:2.2×(√2+√2)海里 (1海里=1.852Km)
より、約11.5Kmとなります。(国土交通省:海難審判所資料等による)
これ以上離れると、光(もしくは電磁波)の性質である直進性のために、光は大気圏へと減衰しながら飛び去り計測はできません。
では11.5Km以上離れたら2点間は計測できないのでしょうか?
大丈夫です。ただ、直接測ることはもはやできませんが、2点の緯度経度から計算する方法が存在します。この緯度経度に関しては、今はGPS衛星により、軍事的に問題のある場所を除けば、5章で述べたように、どこでもいつでも容易に取得することが可能です。
続いて、地球上の2点の緯度経度からその間の距離を計算する方法について説明します。
それが、ヒュベニの公式(図6.1)です。
地球を楕円体として取り扱っており、比較的簡単な式で高い精度で算出可能です。

図6.1 ヒュベニの公式
ここで重要な定数は長半径、短半径、第一離心率です。
今はGRS80(世界測地系)が標準となっているので、その値を使用します。
即ち、その値とは
長半径a = 6378137.000m
短半径b
= 6356752.314140m
(第一離心率e)^2 =
0.00669438002301188 (^2
は二乗を表す)
です。
参考HP:http://yamadarake.jp/trdi/report000001.html
7.幾何学により地球の大きさを計算
6章でP点とQ点の緯度経度からPQ間の距離が既知のものとなりました。この章では地球を真円として考え、その後、なぜ地球の大きさを計算できるのかを解説していきます。
古代ギリシャの時代は、地球上の既知の情報を円の性質に適用して地球の大きさを計算しました。
しかし、それでは場所が限定されてしまい、どこでも計算できるわけではありません。
なかなか身近に感じられません。エジプトのナイル川沿いの話ですから、遥かに離れた日本にいるわたしたちにはピンとくるはずもないわけです。
そこでもう少し踏み込んで、中学で習う図形(平行線の公理や相似など)と三角関数の一部(tanθ)を利用しながら、この日本で
地球の大きさを測定するための解説をしていきます。
球面上では2点PQ間の距離は球の中心を中心としPQを通る大円上の弧で表されます。これが最短です。
例えば、飛行機の最短飛行ルートはこの弧に沿ったものとなっています。
図7.1の球面は地球表面をイメージしたものです。
地軸の傾きは23度26分、北回帰線は北緯23度26分の緯線です。
球面上の2点PQを通る大円が太陽光と平行になる位置はすべて夏至を迎え、Q点のグノモンの影も真北に向かいます。
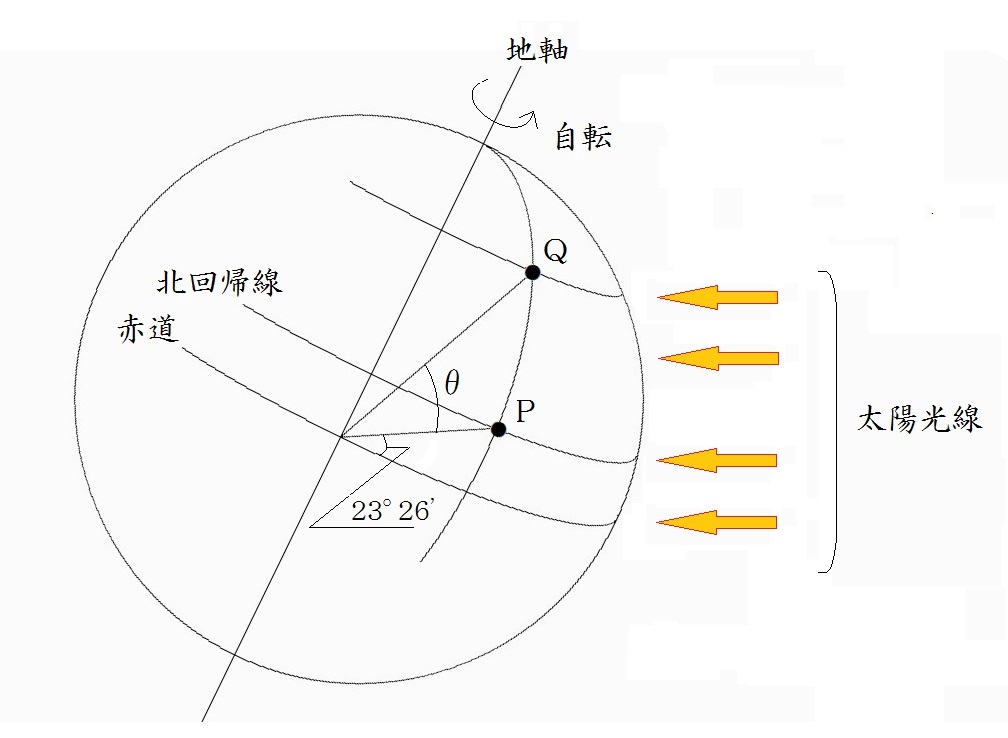
図7.1 球面上の2点間の距離
但し、北回帰線上のP点の影は0cmとなります。それが図7.2です。図中のグノモン(日時計の垂直棒)は誇張して大きく描いてあります。

図7.2 PQを通る大円と太陽光線が平行
地球と太陽の大きさの比は約1:109です。このため太陽からの光線は地球に対しほぼ平行に入ってくると考えて問題ありません。そこで夏至のときの図7.2のP点、Q点、グノモンを拡大すると図7.3のようになります。
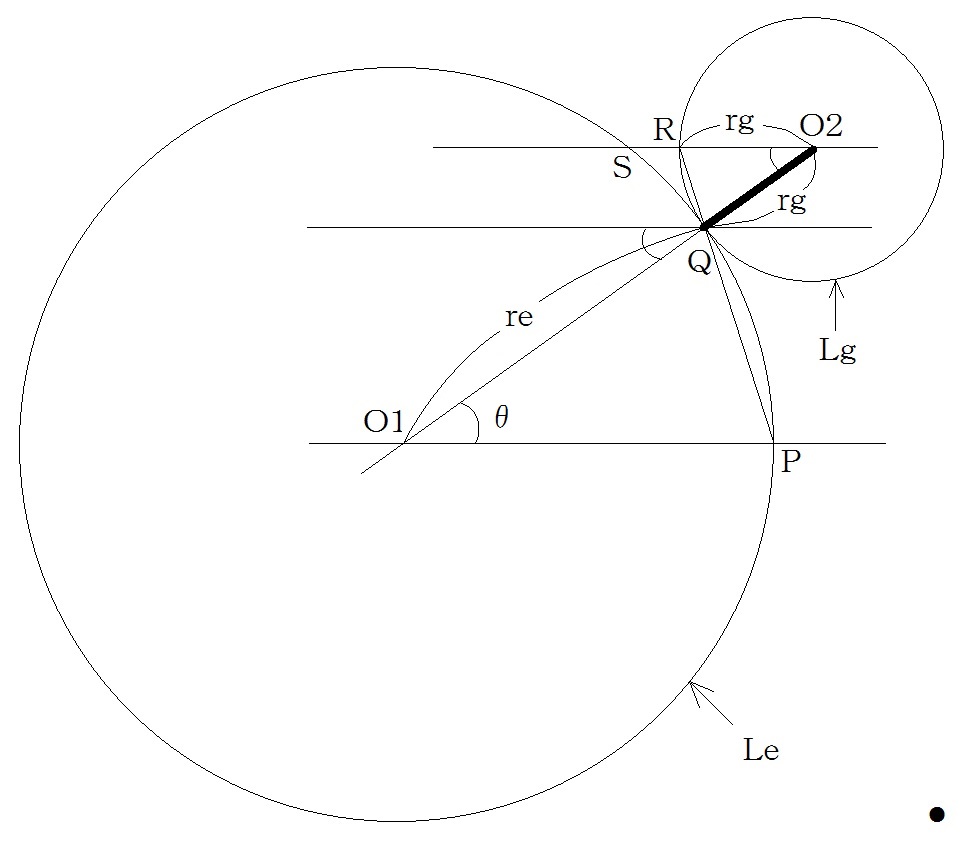
ここで
O1:地球の中心
re:地球の半径
Le:地球の円周
O2
:グノモンの長さrgを半径とする円の中心
rg:グノモンの長さ
Lg:グノモンを半径とする円の円周
Lsh=SQ:グノモンの影の長さ
とします。
図7.3 P、Q周辺の拡大図
以下で、球体(地球)の半径と円周長の計算式を求める方法を解説していきます。この内容は、三角関数以外は中学3年生で習う図形の知識で十分理解可能です。自分で図を描きながら気楽に読み進めてください。(解き方はいくつかあります。)
図7.3のように各交点をP、Q、R、Sとすると、SQはグノモンの影の長さLshをあらす。
図7.3において、Qを通ってPO1と平行な直線との間の錯角は等しく、さらにO2を通ってPO1と平行な直線との錯角も等しいので ∠PO1Q=∠QO2
R=θ が成り立つ。
また、∠QPO1と∠QRO2との間も錯角で等しく、∠O1QPと∠O2
QRは対頂角の関係で等しい。
したがって、△QO1Pと△QO2
Rは相似。
よって、辺RQ:辺PQの比は弧RQ:弧PQに等しい。
即ち、RQ:PQ=弧RQ:弧PQ
(=rg:re)
次に円O1、円O2
において同じ円周角については
弧RQ:弧PQ=Lg:Le
が成り立つ。
これらをまとめると次のようになる。
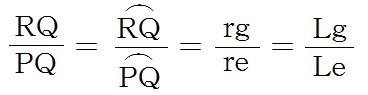 ・・・(1) ・・・(1)
ここで未知のものはre(地球の半径)とLe(地球の円周)であるが、この比例式からいづれも求めることができる。
(1)の第2、4項より、地球の円周Leは

となる。
ここで三角関数を利用すると、グノモンの影の長さ(実測)は
SQ=Lsh=rg・tanθ (θの単位はラジアン) (*1)
である。よって、

即ち、グノモンと太陽光線のなす角度θは

となる。一方、弧RQは
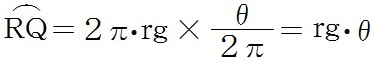
と表される。よって、地球の周長Leは
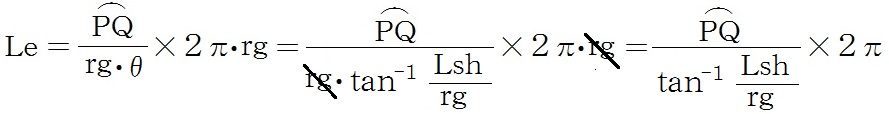
ここで、弧PQ(P、Q間の距離)はソフトウェアにより求まり、Lsh(グノモンの影の長さ)は実測値、rg(グノモンの長さ)は既知であるから、地球の円周長Leが求められるのである。
また(1)の第2、3項より、地球の半径reは
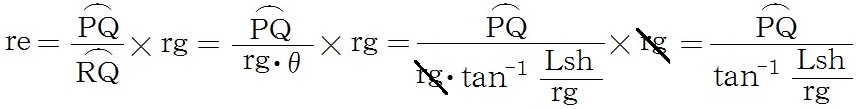
と求めることができる。
以上をまとめると、球体(地球)の円周長Leと半径re
は
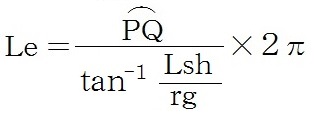
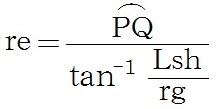
となる。
注)
(*1)三角関数について
三角関数は高校で習う内容だが、形式的には難しいものではない。
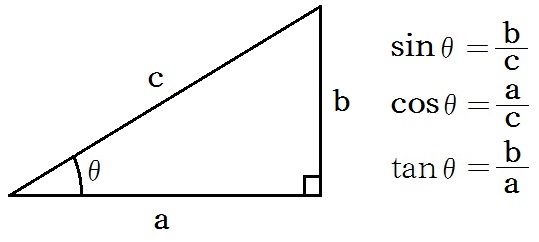
下図のような直角三角形において、各辺をa,b,cとし、辺aと辺cのなす角をθとしたときに辺の比として定義されるものである。sinはサイン、cosはコサイン、tanはタンジェントと読む。
(尚、ここでは0°<θ<90°とする。)
8.結果を予測する
ここで、自分の住所におけるθの値を予測してみる。
自分の住所をQとすると、(1)の第1、4項より
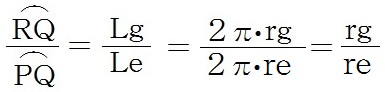
よって
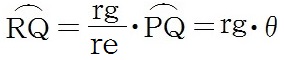
となる。ここで、弧RQ=rg・θを利用した。
これよりθは
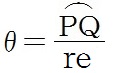
と簡単になる。
これに地球の半径re=6370km、弧PQ=1463kmを代入すると、
θ=1463/6370=0.23 rad=13.3
°
このときグノモンの影の長さLshは、
Lsh=rg・tanθ
で計算できる。
θ=13.3°、rg=20cmを代入して
Lsh=20・tan13.3°≒4.7
cm
となる。
グノモンが20cmのとき、太陽光とグノモンのなす角度θは、13°〜14°、グノモンの影の長さは4〜5cmになると予測できる。
|