|
B.検電現象 −
15.これまでの一般的な決定において、角柱状物体に注意を限定してきた。
また、横軸にとったその中心線は直線であった。
しかし、何らかの方法で、一定の曲線を描く伝導体を考え、
続いて、伝導体の湾曲した中心線上に横軸をとるならば、
これらの考え方は十分に意味を持っている。
ボルタの回路は、その真の性質から直線に拡張されることはめったにないので、
この観測により、以上の式はそれらに完全に適用することができる。
この点を予測することで、直ちにもっとも単純な事例へと進めることができる。
それは、角柱状伝導体が同じ材料で全て作られており、さらにそれ自身後方に曲げられ、
2つ端が接触するところの電圧を考える、ということである。
たとえ自然における事例に、この想像上の事例と似たものがなくとも、
それは、実際自然に必ず生じる別の事例の取り扱いにおいて大いに有益なものとなるだろう。
そのような角柱状物体のどの場所でも、検電力は
11節で見出した微分方程式(a)により減少させられるだろう。
この目的のため、われわれはそれを積分し、
さらに、問題の別の条件に従い、
積分をするときに入ってくる任意の関数を決定しさえすればよい。
問題の性質に従い、
方程式(a)から1つまたは2つの項を省くことにより
問題は一般的に大いに簡略化される。
このようにして、ほぼボルタの作用全てについて、
その現象がそれらの根源において直ちに恒久不変である、
ということができる。
それゆえ、この事例では、
検電力は時間とは独立しており、
その結果、方程式(a)は次のように変化する。
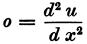
しかし、この最後の方程式の積分は
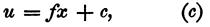
である。
ここで、fとcは(決定されるべく残った)ある定数である。
その結果、この方程式(c)は、等質の角柱状伝導体において
「空気による外転(訳注1)を受けない」(周囲の大気がボルタの回路に影響しない)事例全てにおける電気の拡散の法則を表わし、さらにその作用はもはや時間と共に変化しない。
(訳注1)abduction=外転、ガルバーニ電気回路の数学的研究ではアースに落とすことであったが、ここでは異なる。外転は外からの影響で、内転は外への影響として使われている。
実際のところ、これらの状況はボルタの回路によく付随してくるものなので、
われわれはその説明のため、長めに時間を費やすことになるだろう。
伝導体の両端に発生する電圧により、定数の一つを決定することができる。
それは各事例において不変かつ既に決まっているものとして見なされねばならない。
例えば、物体の中心線のどこかに横軸の原点を仮定し、
横軸上の、一方の端の位置をx1で表わすなら、
そのとき、そこの検電力は方程式(c)により、
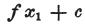
となり、同じ方法によりもう片方の端の検電力が得られる。
つまり、横軸上のそれをx2で表わすと、
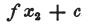
となる。
次に、与えられた電圧または検電力の差をaとすると、
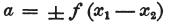
を得る。
(訳注)以上のイメージ図
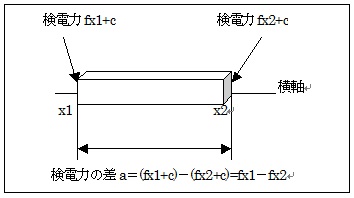
一方、x1−x2は明らかに、+または−の、角柱状伝導体の長さを表わす。
これを ℓ とすることで
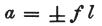
を得て、そこから定数fは決定されるだろう。
次に、方程式(c)で見出した定数の値を導入すれば
それは次のように変換される。
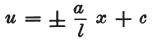
(訳注)方程式(c)に、f=±a/ℓ を代入すると、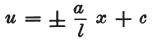 となる。
となる。
横軸上の伝導体の端が最大の検電力を持つ場合は+の値をとり、反対の場合は−の値をとる。
ここで電圧aに付いた符号±は分かりにくいかもしれない。
そこで、この仮定の下で一般化した表現をすると
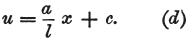
となる。
定数cは概して未知の定数である。
それは外部の影響により任意に変化するので、伝導体内での電気の拡散を容認するものである。
即ち、そのような方法で、それは伝導体内のあらゆる場所に一様に分布する。
この定数に関するさまざまな考え方の中に、ボルタの回路に特に重要なものが一つある。
即ち、完全な伝導体と、ある場所で接続された回路を仮定すると、
そのために、検電力は
それが絶えずその場所で破壊されたかのごとく見なされるはずである。
この点の横座標をλ(さらに電圧をo)とすると、方程式(d)により、
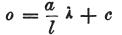
となる。
定数cを決定し、さらに同じ方程式(d)にその値を入れることで、次の式を得る。
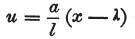
これで横軸上λの場所で接触させた、
長さ ℓ 、電圧aのボルタの回路の検電力は、
どの場所でも検出されるだろう。
もし外部からボルタの回路へ、何らかの一定で完全な内転が
見かけ上、恒久的な外転または抽出の代わりに与えられたなら、
そのために、横軸λ上にある検電力は、その与えられたエネルギーをも考慮しなければならない。
そして、そのエネルギーをuと呼び、定数cの決定のために、
次の方程式
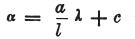
を得る。
また別の位置での回路の検電力を決定するため、さらに次の式を得る。
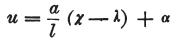
かくして、検電力が外部の環境により回路のある場所に示されるとき、
いかにして定数cが決定されるのかが分かった。
しかし、次に問題が生じる。
定数が完全にこの回路を左右するとき、
われわれはどのくらいの値を定数とすればよいのか?
さらにその結果、その値がもはや外部の環境に由来するようなことはないのか?
ということである。
その答えは
いつも2つの電気は同時発生的、且つ前の中性の状態から等しい量を生じる、
という考え方の中に見出される。
それゆえに、
今の性質の単純な回路−それは完全に中性に作られ、且つ周囲とは分離されている−は、
接触場所の各端では、等価だが電気的状態が逆であると思われる、
と主張されるだろう。
そこから、それらの中心が中性であろうことは自明である。
しかしながら、同じ理由から、
その回路が、何らかの環境の変化により普通の状態ではいられなくなったとき、
再び変化が生じるまで、間違いなく異常な状態を保持するだろう、
ということは明らかである。
よって、これまで考えてきたような単純なボルタの回路の特性は、
方程式(d)からまったく明らかなように、
根本的には、次の内容から成り立つ。
その答えは
いつも2つの電気は同時発生的、且つ前の中性の状態から等しい量を生じる、
という考え方の中に見出される。
それゆえに、
今の性質の単純な回路−それは完全に中性に作られ、且つ周囲とは分離されている−は、
接触場所の各端では、等価だが電気的状態が逆であると思われる、
と主張されるだろう。
そこから、それらの中心が中性であろうことは自明である。
しかしながら、同じ理由から、
その回路が、何らかの環境の変化により普通の状態ではいられなくなったとき、
再び変化が生じるまで、間違いなく異常な状態を保持するだろう、
ということは明らかである。
よって、これまで考えてきたような単純なボルタの回路の特性は、
方程式(d)からまったく明らかなように、
根本的には、次の内容から成り立つ。
a.そのような回路の検電力(ポテンシャル)は
伝導体の全ての場所で、頻繁に、(常に同じ量、同じ範囲で、)変化する。
しかし、2つの端は接触状態にあり、
それは、事実、一方の端から他方の端へ全電圧の大きさまで急に変化する。
b.回路のある場所が、何らかの環境の変化によりその電気的な状態を変えられたとき、
回路の他の場所もすべて、同時に且つ同量、変化する。
16.次に、2つの部分PとP’から構成されるボルタの回路を考えたい。
接触する2つの点でそれぞれに電圧が発生し、さらにこの事例は熱回路を含む。
P部分の検電力をu、P’部分の検電力をu’とすれば、
これまでの節により、この事例では方程式(c)が2度繰り返されことに注意して、
P部分に対して、
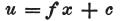
次にP’部分に対して、
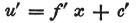
となる。
ここで、f,c,f’,c’は
この問題の特殊な環境(条件)に由来するある定数であり、
各方程式は、
方程式が成立するその部分に、横座標上にある限りにおいて、
有効である。
次に、P部の接触場所のひとつを横軸の原点とするならば、
この部分における横軸方向を内部へ向かう方向に仮定し、
さらに、P部の長さを ℓ で、またP’部の長さを ℓ’で表わし、
最後に、x=ℓ の接触場所でのuとu’の値をu2’とu1で表わす。
このとき、
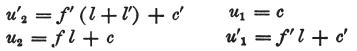
を得る。
次に、x=oとなる接触場所に生じる電圧をaで、
また、x=ℓ となる接触場所に生じる電圧をa’で表わすならば、
さらに、これが最後だが、等質性のために、
個々の接触場所の電圧が、
問題の場所にある一端の検電力からもう一端の検電力を差し引くときに得られる値を
常に表わすなら、
突然の変化が発生する前に、横軸は下降する。
−(この一般的な法則が、前節で進めたそれを含む、ということを認めることは難しくない。
そして、事実、
より大きい検電力からより小さい検電力を引いた検電力がその横軸方向に生じることにより、
そのような接触場所の電圧は+として、反対の場合は−としてみなされる、
ということ以外何も表わさない。
しかしながら、
あらゆる+の力は、あらゆる−の力よりも大きいものとして受け取られるべきである、
ということを見落としてはならない。)
ここで、
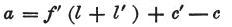
と

を得る。
これより直接的に、
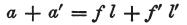
となる。
しかし、次に各接触場所において、χとωが伝導力(=導電率)とP部の断面を、
また、χ’とω’が伝導力(=導電率)とP’部の断面を表わすとき、
13節で展開された考え方によれば、
そこには、条件付方程式
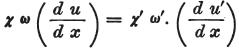
が生じる。
ここで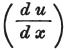 と と は接触部分における は接触部分における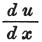 と と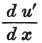 の値を表わす。 の値を表わす。
しかしながら、
この回路の1つの部分における検電力の決定のため、この節の始めの方程式から、
それぞれに許容されるxの値を得る。
ここで、
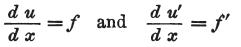
(を代入して)問題の条件付方程式を変換すると
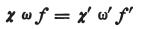
となる。
これより、方程式

が正にこの電圧を導き出す。
続いて、次のようにfとf’の値を見出す。
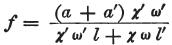
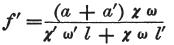
そして、これらの値の助けにより、
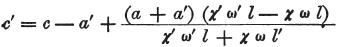
を得る。
ゆえに、P部における回路の検電力は次の式で表現される。

そしてこの方程式により、P’部における回路の検電力は
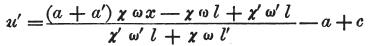
となる。
ここで と
と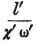 の代わりにλとλ’を入れると、
の代わりにλとλ’を入れると、
次のようにより簡単な形式がこれらの方程式に与えられる。
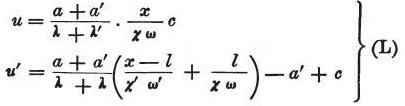
これらの方程式の形から、
導電率または断面の大きさが2つの部分で同じとき、
uとu’についての式は、
導電率または断面を表わす文字がすっかり消えること以外に何の変化も受けない、
ということが直ちに解る。
|