同じ太さの電線で作られた異なる金属の２つのガルバノメータの極端な動作（電流）は、これらの金属の導電率と比率がお互いに同じであることを示すだろう。

そして、同じ金属の電線で作られた２つのガルバノメータの極端な動作（電流）は電線の断面とそれぞれ同じ比率となる。

ガルバノメータに関するこれらのさまざまな特性すべては、−部分的には、他の人々により行われた実験で、また著者の実験でも−実験により見い出されるべくして示されてきた。（編注1）

熱回路におけるこの問題についてなされた最も新しい実験は、異なった（また、ある意味では逆の）方法で、既に、縮小長の式から以上のことを結論づけられる結果を示していた。

つまり、熱回路における電圧の合計は通常の水回路のそれよりも遥かに弱いのである。

そして、私は１つの暫定的な比較により次のことを確信した。

つまり、加熱効果に関して、もしそれらが確定的に予言されることになっているならば、数百の精選された、簡単な熱回路によるボルタの（電池の）結合が、何らかのエネルギーの化学的な影響のために、遥かに大きな装置を必要とする、ということである。

疑いなくこの予測を決定する実験は、ここに提示してきた理論に対し、新しいものと重要でないはずのない確証をあたえるだろう。

分割された、または派生的な回路．

−これまでの検討は、ボルタの回路がある位置で２つもしくはそれ以上の部分に分割されるときに、
維持されるその過程を示すのにも十分である。

この目的のため、次のことを思い出そう。
即ち、式　　を発見した時に、

ボルタの回路の同種の部分における電流の強さは、どこにおいても、その部分の両端に存在する電気の力（ポテンシャル）とその縮小長の比によって与えられる、という法則をも手に入れた。

この法則が、回路が全く分割されていない場合に対し、前に述べたことを前進させたに過ぎない、というのは事実である。

しかし、おのおのの角柱部分の全断面において、追加され、且つ差し引かれた電気の量に由来するという非常に単純でよく似た考え方は、同じ法則が、回路を分割した場合に個々の分割部分をうまく維持している、ということを証明するのに十分である。

例えば、縮小長がλ、λ’、λ’’である、３つの部分に分割された回路を仮定しよう。

そして、これらの各場所において、未分割の回路と１つの分割部分が同じ電気の力を保有するので、
電圧はそこに発生しないのであり、さらに、これら２つの場所の電気の力の差により示すこともない。

そのとき、先の法則にしたがって、３つの分割部分それぞれの電流の強さは

　　
となる。

かくして、３つの分割部分における電流はそれらの縮小長に反比例する、ということが直接的にいえる。

ゆえに、これら３つの（部分の電流の）合計が互いにわかっているとき、それぞれの値がわかるだろう。

しかし、３つの部分全ての（電流の）合計は、明らかに回路の非分割部分のどの場所における電流の強さにも等しい。

つまり、その一方で、いまだ継続して想定される回路の永続的状態は、維持されないだろう。

もし以上の考え方から帰結される結論をこれに関連づけるならば、
言い換えれば、即ち、電流の大きさと回路の各同種の部分の性質が、
電気（電圧の低下）の分離を表現するための直線と一致するディップを与えるならば、
以下のことを確信するのである。

即ち、回路の非分割部を示す（電気の）分離の図が、その内部の電流が同じ強さを保つのと同じ強さを維持しなければならない、またその逆も真なり。

このようにして、必然的に非分割部における電流の変わりやすさは、この部分の両端の電気的な力の差が一定であることによるのだ、と推測するに至る。

［　１つの重要な法則は、回路内に配置された２つの並列の伝導体間の電流の分配を規定する、
ということである。

もしそれらが同じ性質で、同じ直径で、同じ長さ、−例えば、２つの同じ電線で達成される状態−であるならば、その電流がそれらの間で等しく分割されるということは明らかである。

しかし、もしそれらが同じ性質であり、また同じ直径である一方で、異なった長さであった場合、
ここで一つの長さをｍ、もう一方をｎとしよう、そのとき、それぞれを通過する電流の比は、それぞれの長さと逆なのであり、全電流の強度は、ｍとｎの長さの２つの電線ではなく、あたかも１本の電線が長さ　　の回路に配置されたが如く、そこに流れる電流と同等となる。

一般的に、もしａとλが回路に並列に挿入された２つの伝導体のそれぞれの抵抗を表わすならば、
２つの伝導体の全抵抗は、　によって表わされるはずの１つの伝導体の抵抗と同じである。

２つの伝導体については、それらの特性や長さ、断面積、またはこれら３つの互いの条件が異なるかもしれない。

ただ、それらがともに金属であるか、さもなくば流体であることが必要なのである。

ド・ラ・リーブ　（編注2）］

もしいま、個々の分割部分の代わりに、その電流と電圧の強さがまったく変わらない回路に
持ち込んだ縮小長Ａの１つの伝導体を仮定してみると、そのとき、まさにこれまで述べてきたことに従えば、その両端の電気の力の差は、常にａのままであり、
その結果、

　
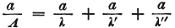
または

　
でなければならず、これはΛの値を決定するために役立つ式なのである。

（編注1）シュバイガーの年鑑、1826年　第二巻、と1827年
（編注2）電気学の論文：ド・ラ・リーブ　第二巻　84ページ　1856年