２１．全てのボルタの回路に共通な現象は
その検電力が絶え間なく、しかも任意に支配されているような
急な変化にある。
この現象は、以前に明らかにしたそのような回路の特性を原因とする。
既に発見したように、ボルタの回路の各点は、
単純なそれ（ボルタの回路）が受けるのと同じ変化を受けるので、
あるときは前者に、またあるときには後者に
ある場所での検電力という数値を与える必要がある。
これらの変化の間に、物体（同士）を接触させることで
例えば、検電力を破壊したり、
またあるときは、回路のある場所でそれをゼロ値にすることで、
さらに、またあるときは回路の別の場所でそれをゼロ値にすることで、
ゼロ電圧を生み出すことが出来る、ということは注目すべきである。
しかしながら、その大きさには、電圧の大きさ本来の限界がある。
これらと共に直接接触させる（ことで生じる）現象にはまた別の段階がある。
例えば、検電力が、与えられたボルタの回路ｒ内に拡散されるところを空間とし、
また、直接外部の物体Ｍと接触している回路のある場所の検電力をｕとし、
さらに、物体Ｍに接触させる前の状態で、
同じ回路の同じ場所の検電力を記号ｕ’とするなら、
ｕ’−ｕは明らかにこの場所に生じた検電力の変化分である。
その結果、さらにこの変化が回路の他の場所全てで均等に生じるので、
ｒ（ｕ’−ｕ）は全回路中に生じた変化分が含む電気の量であり、
したがって、それは物体Ｍ内を通過した電気の量である。
次に、平衡状態で、
検電力が、それが発生する物体Ｍの全ての場所で同じ強度であり、
また、それが物体Ｍ内に拡散されるその空間をＲで表わすとすると、
その検電力は明らかに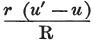
である。
しかし、この力は平衡状態においてｕ’に等しく、
その回路の場所は、当然、Ｍと接触状態しており、
この接触場所に新たな電圧が生じないときである。
それゆえに、この仮定の下で、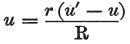
となる。
そこから、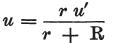
を見いだす。
この方程式から、物体Ｍの検電力は、
接触前、その場所でゼロであったそれより、常に小さいだろうと結論できる。
そして、その両者が互いにより近ければ近いほど、ｒがＲに比べてより大きくなるだろう。
（r：ボルタの回路、Ｒ：検電力が物体Ｍ内に拡散する空間 ）
ここで、Rが一定の大きさなら、検電力ｕとｕ’の互いの関係は
単に電気がその回路で占有する空間の大きさに依存することになる。
その結果、その回路の容量を増やすことにより、
（言い換えれば、普通に寸法を大きくするか、もしくは別の物体とどこかで結合することにより）
物体Ｍの検電力をその最大値により近づけることができる。
それらが単なる電気の伝導体であるとき、
この作用はは、少しもこれらの物質の性質に依存するように見えず、
新たな電圧を生じないばかりか、それらの大きさにも依存しない。
その接触させた物質が計り知れない巨大な空間を占有するなら、
−ただし、その回路の場所を問わない推論の時に生じる事例である−
物体Ｍの検電力は
それに接触した回路のその場所が有する検電力に常に等しいだろう。
コンデンサの作用とこれらの作用とを関係付けるには、
容量がＲで、充電量がｍのコンデンサは、ｍＲの大きさの一般的な伝導体と同じと考えねばならない、
と覚えておくだけで良い。
さらに、その検電力は一般的な伝導体のそれのｍ倍であるという違いがある。
それゆえに、コンデンサの検電力をｕとすると、
それは検電力がｕ’の回路の場所に生じ、
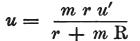
を得る。
（ｕ’：物体Ｍに接触させる前の、同じ場所の同じ回路の検電力＝電圧）
（r：ボルタの回路、Ｒ：検電力が物体Ｍ内に拡散する空間 ）
これより、
ｒがｍＲに比べて非常に大きいとき、
コンデンサは接する場所の検電力のｍ倍を示すだろう、
ということが結論される。
（訳注： ｒ＞＞ｍＲのとき、近似計算によりｒ＋ｍＲ≒ｒとなる。よってｕ≒ｍｒｕ’／ｒ＝ｍｕ’となる。）
しかし、それは即ち、
ｒがＲに等しいかそれより小さければ、その作用は弱まるだろう、
ということである。
したがって、どこであろうとも回路に接したその物体は、
それらの大きさに応じて、
コンデンサの（検電力の）表示値を最大に近づけるだろう。
そして、（物体の）ある場所に接触した回路は、絶えず
コンデンサ内に（電気の）最大の増加をもたらすだろう。
先の決定は
コンデンサの１つの電極板が、仮定として常に接触したままであること
を仮定とする。
次に、絶縁されたコンデンサの２枚の電極板が
ボルタの回路の別々の場所に接続されている場合を検討してみよう。
第一に、絶縁されたコンデンサの２枚の電極板は、
それらが接触している回路のさまざまな場所が、ボルタの作用の特殊な性質を無条件に要求する、
それぞれ同じ自由な電気を帯びている、ということは明らかである。
その結果、
ｄが回路の2箇所の検電力の差を
さらに、ｕがコンデンサの１つの電極板の自由な電気を表わす場合、
ｕ＋ｄはもう一方の電極板の自由な電気を表わす。
そして、すべては、
コンデンサの電極板内に存在する既知の自由な電気から
−事実、それら（自由な電気）はこれら（電極板）の中に存在する−
の発見次第であろう。
例えば、この目的のために、
電極板内の実際の電気の強さ−その自由な電気はｕ＋ｄである−をＡとすると、
Ａ−ｕ−ｄは同じ電極板に保持される一部の電気を表わす。
同じ方法で、
Ｂが電極板内の実際の電気の強さを表わすとき、
Ｂ−ｕは、自由な電気がｕである電極板内に保持される電気の一部を表わす。
次に、１つの電極板に保持されている電気と
もう一枚の電極板の実際の電気の間の関係をｎで表わすなら、
次の２つの方程式
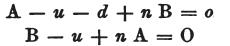
となる。
値ＡとＢはその結果、次のようになる。
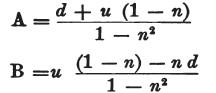
しかし、ｍが電気の充電量を表わすなら
コンデンサの理論から、それは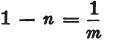
であることが良く知られている。
それゆえに、式Ａ、Ｂにおいて、
の代わりに
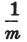を、
また同時に、ｎの代わりに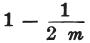
を代入すると、
ｍがよくありがちな非常に大きな数であるとき、
次の式を得る。
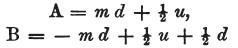
一方、ｍは非常に大きな数だが、ｎはｄよりは大して大きくないとき
ほとんど気にせずに、
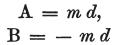
と置いてよい。
これは、周知の法則を表わしている。
つまり、それは次の通りである。
ボルタの電池の異なった２つの位置から、
絶縁されたコンデンサの２つの電極板へと（電線が）つながっているとき、
あたかも一方の電極と（それと繋がる）バッテリの相応する位置が
仮に接触しているかのように、それぞれの電極板が同様に充電される。
同時に、ｕがもはやｍｄに対し無限小と見なすことができないとき、
この法則は正しくないということを、この考え方は示している。
例えば、ゼロ電位を維持するため、
（ボルタの電堆の）下の極が大地（アース）に接続されている場合、
ボルタの電堆−それは莫大な数の電極で構成される−の絶縁された上の極に近い２点が、
コンデンサの電極板に接触したとき、
この事例が起こるだろう。
これまでに分かった、
ボルタの回路が外部の物体に電気を伝える方法は、
残念だが、かなり異なった種類の、さして多くの人の興味を引く研究となるだろう。
というのは、
動いている電気が物体の内部を貫通し、
それにより、その量は、物体が占有する空間に依存するということが、
何の疑いもなく、理論的にも実験的にも認められるだろうからである。
一方、静電気が物体の表面に蓄積するということについては、
十分に確認可能であり、
その結果として、その量は表面の領域に依存することがわかる。
しかし、この点から、
閉じたボルタの回路では、前述の式におけるｒ（r：ボルタの回路と定義）が、回路の大きさを表わす
ということになるだろう。
一方で、開いたボルタの回路では、
その表面の大きさは実験により容易に決定されるだろう。
２２．これまで、回路には周囲の大気が影響せず、
またその恒久的な状態（安定状態）に既に到達したもの
として見てきた。
そして、その回路に関連した現象が豊富で重要性がある、
という点に価値が有るものとして、その回路を取り扱ってきた。
しかし、それとは異なる回路を放置したままにしておく訳にはいかないので、
最も単純な事例で追いかけることができる理論を示し、
さらに、たとえ遠くとも、従うべき進路を指し示そう。
ガルバーニ回路における大気の影響を考慮するなら、
項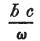
を、１１節の方程式（ａ）の項
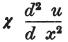に追加しなければならない。
そのとき、既に安定状態になっている回路については、
なので
次の方程式
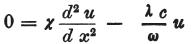
を得る。
また、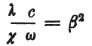
と置けば
を得る。
この方程式の積分は
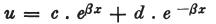
である。
ここで、ｅは自然対数の底、ｃ，ｄは問題の他の環境から決定されるある定数を表わす。
次に、回路の全長を２ℓとし、
さらに励起点から等距離にある回路のその場所に、横軸の原点を固定し、
その上、励起点に存在する電圧をａで表わすなら、
次の式
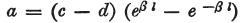
を得る。
ここで前に見出した方程式を書くと、次のようになる。
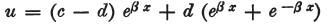
（訳注）次の式の導出について
u ＝ c・ｅ＾βx ＋ d・ｅ＾-βx ＝
c・ｅ＾βx ＋（d・ｅ＾βx −
d・ｅ＾βx）＋d・ｅ＾-βx ・・・?@
ここで、数学的テクニックを用いている。d・ｅ＾βx − d・ｅ＾βx
＝０、つまりA−A＝０である。
次に?@の１項＋３項より、
c・ｅ＾βx− d・ｅ＾βx＝（c−
d）・ｅ＾βx
?@の２項＋４項より、
d・ｅ＾βx ＋d・ｅ＾-βx＝d・（ｅ＾βx
＋ｅ＾-βx）
よって、?@は
u ＝（c− d）・ｅ＾βx＋d・（ｅ＾βx
＋ｅ＾-βx）・・・?A
となる。一方、
ａ＝（ｃ−ｄ）（ｅ＾βℓ
−ｅ＾-βℓ）を変形して、ｃ−ｄ＝ａ／（ｅ＾βℓ −ｅ＾-βℓ）を得る。
これを?Aに代入すればｕに関する以下の式を得る。
さらに、ちょうど見つかった値をｃ−ｄに代入すると、
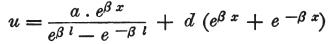
を得る。
次に、他の定数を決める場合、
励起点に生じた２つの検電力の合計が分かっており、それはｂに等しく、
さらに回路の検電力がその場所のいづれかで与えられるとき、
その事例が常に発生すると仮定すると、
方程式
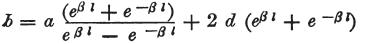
を得る。
さらに、代入と適正な約分の後に
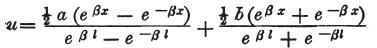
を得る。
例えば、ｂ＝０の場合、第二項がすっかり消えて、
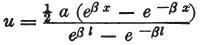
に変わる。
回路の全領域で等質且つ角柱の特徴を保っている
これらの方程式は
上の式でβ＝０のとき、再び変化する。
これまでに与えられた環境下では、
その回路への大気の影響は検討の対象外である。
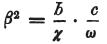から、
大気の伝導力（＝導電率）が
回路のそれに比べて小さければ小さいほど、また比
が小さければ小さいほど
ボルタの回路への大気の影響はほとんど無い。
しかし、比
は
大気に囲まれている伝導体の１個のディスクの表面と同じディスクの容量の関係を表わす。
（ω：円柱状又は角柱状の物体の断面、ｃ：未知の定数）
それ故に、
は常に無限に小さくなければならないということを表わすはずである。
しかしながら、ここでは数学的だけでなく、物理的な決定（に至るため）の処理がされていない。
というのは、厳密にとらえるなら、
ｃは表面だけでなく、大気が直接影響する回路のディスクの部分（円周部分）も意味しない上、
実際のところ、
ωが回路を絶えず通過する電気が横切る、回路のディスクの一部分であるという事の外、
何も意味しないからだ。
それゆえに、一般的には、ｃは実際のところ、比較できないほどωよりも小さいかもしれない。
しかし、
そこで、電流は最大の困難を伴って前進するのみで、
さらに、それは非常に遅いために、多かれ少なかれ、乾電池内の場合と同様に
ｃの大きさは、前の節で述べたことにより、ほとんどωに等しくなる。
つまり、
同時発生する環境により変えられる、疑いようのない段階的な遷移は、
突然に変化する電流に特有の性質と完全な平衡状態にある電流に特有の性質から
発生するに違いない。
そのとき、ここには、広範な領域が未来の研究に開かれているのである。