|
殿下との私の書簡の現在のテーマはあまりに退屈でお疲れになられているのではないかと、私は心配し始めています。わたしはそれに大した時間を費やしていない上、あまり興味が無い話題を度々繰り返す必然性から救出されるかもしれません、私はすぐにこの配達により3つの手紙をあなたに送ります。
それを引き受ける私の目的は、
音楽家自身がほとんど全く知らない、
音楽の音の真の起源を視覚化することであった。
それは、全てのこれらの音の知識から恩恵を受けている理論のためではなく、
むしろ彼らの耳に非常に効果的に作用する純粋な和声の秘密の力のためである。
即ち、かれらは、
もし私がそれを言うことを許されるならば、
たとえかれらが、これまでかれらの正しい判断に関して完全に同意されなかったにしても、
かれらは実際に使用している音を受け入れることを強いられてきた。
私が証明してきたように、主要な和声は結局、数を少なくすることができる。
そして、数字2が複数のオクターブのみを与えるということが注目されてきた。
ゆえに、例えば、音Fを固定することにより、われわれは音f、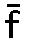 、 、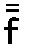 、 、 を導く。 を導く。
その後、数3が前の連続とは1/5異なるC、c、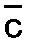 、 、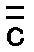 、 、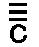 を与える。 を与える。
そして、この同じ数字3の繰り返しが再び最初の第五、即ち、G、g、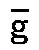 、 、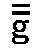 、 、 を与える。 を与える。
最後に、この数字3の第三の繰り返しが音D、d、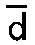 、 、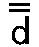 、 、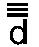 を遥か先に加える。 を遥か先に加える。
そのとき単純化された主要な和声は、数3の繰り返しを排除することを禁止するように見える。
従って、これまで、われわれはオクターブ毎に次の音を手にしている。
 は確かにたいして豊富な音楽を与えないだろう。 は確かにたいして豊富な音楽を与えないだろう。
しかし、これらに加えて、数5を取り入れてみよう。
そして、Fがたった1つの振動を発する間に、5つの振動を発する音を観測するだろう。
それから、fは同時に2振動を出し、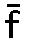 は4振動を、
は4振動を、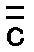 は6振動を行う。 は6振動を行う。
その時、問題の音は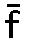 と と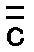 の間にある。 の間にある。
それは、音楽家が文字 により示し
、 により示し
、
音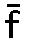 と共にgreater third(3度以上)と呼ばれる和音であり、 と共にgreater third(3度以上)と呼ばれる和音であり、
さらに4:5の非常に単純な比によって表現されることで、
非常に快適な協和音を生み出すことが発見されている。
その上、音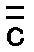 と共に音 と共に音 は、ほとんど前者のように快適な、 は、ほとんど前者のように快適な、
さらに27:32の比で表わされるlesser third(3度以下)
と呼ばれる5:6の比を含む和音を生み出し、
そして、第一のものとの違いは、ほとんど聴覚には知覚不可能であるということである。
他の音G、c、dに適用されるこの同じ数5は同じ方法で、
2オクターブ以下で取られるgreater third(3度以上)をわれわれに与えるだろう、
即ち、移調されている音 、
、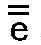 、 、 は、それらの一致している数と共に次の音を与える。 は、それらの一致している数と共に次の音を与える。

音Fsを取り去ると、
あなたはハープシコードのprincipal touch(オルガンの主要音栓の感触)を得るだろう。
つまりそれは、古代人によると、
数2、数3、数5から生じる、ダイアトニック(全音階)と呼ばれる種を構成する。
これらの音のみを認めると、われわれは非常に心地よく変化にとんだ和声と、
音に一致する数のみの単純さに見出される美を構成する条件の下にいるのである。
最後に、再び数5を適用することで、
われわれは、われわれが正に発見した第3の4つの新しい音、
A,E、B、Fsを備えるのであり、
われわれは音Cs、Gs、Ds、Bを手にいれるのだ。
それゆえに、いま、オクターブは音楽で認められた12音を完成するのである。
全てのこれらの音は、オクターブが必要とする度に自身に2を掛けることにより、
それらの起源を3つの数字2,3,5に由来する。
しかし、われわれは第3段階へ3の掛け算のみで、第二段階へは5の掛け算で至る。
第一のオクターブの全音は、
あなたが
どのようにして基数2,3,5がこれらの音の関係を表わす構成の中に入っているのか
を知るであろう
次のテーブルに含まれる。

C音が384振動する間に、Cs音は400を与え、
他はそれらの一致数で印されるのと同じである。
その時c音は同時に384と記された振動数の2倍、即ち768を与える。
そして、次のオクターブの場合、
あなたはこれらの数に2、または4、または8を掛けさえすればよい。
従って、音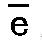 が768の2倍または1536振動、 が768の2倍または1536振動、
音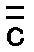 は1536の2倍または3072振動を与え、 は1536の2倍または3072振動を与え、
音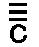 は3072の2倍または6144振動を与える。 は3072の2倍または6144振動を与える。
これらの数2,3、5による音の構成を理解するためには、
前にある数の中の数の間に配置されたその位置が、
それらが互いに掛けらることを意味する、ということが注目されるべきである。
このように音Fsをとってみると、
例えば、2,2,3,3,3,5という表現は、2に2を掛け、
その結果に3を掛け、その結果に再び3を掛け、その結果に5を掛けることを意味する。
さて、2かける2は4、それに3を掛けると12、
それに3を掛けると36、それに3を掛けると108、それに5を掛けると540である。
ゆえに、これらの音の間の差異はそれ自身の間では等しくないことがわかる。
しかし、あるものは大きく、他のものは小さい。
これは真の和声が要求するものである。
しかしながらこの不平等は大したことはないので、
ある音から別の音までの間隔をsemitone(半音)と呼び、
われわれは等しいものとしてあらゆるこれらの相違を見なしている。
そして、このように、オクターブは12の半音に分割される。
多くの現代音楽家は、和声の原理とは反対であるが、
1/5や1/3が全く正確ではないので、それらを平等に使い、
さらにその効果は、あたかもこれらの音がまったく調和していないかのようである。
同様に、かれらは、われわれが半音の同等の利点を手に入れるためには
和音の正確さを諦めねばならないことを認める。
だからといって、ある1つの音から他の音への移調が
どうみても旋律をだめにするということは無いだろう。
しかしながら、かれらは、C音または、半音高いつまりCsで演奏される同じ曲は
相当にその性格に影響を受けることを認める。
それゆえに、いかにそれらを表現するために音楽家がそれらしくしようと努力しようとも、
実際全ての半音は均一でない。
なぜなら、真の和声は、その性質とは正反対の計画の実行に抵抗するのだ。
その上、そのようなものが実用上、既に音楽的な音の真の原点となっているである。
それらは数2、3、5に由来する。
われわれが数7の採用を更に進めたならば、
1オクターブの音程は増やされ、さらに音楽の芸術性はより高度な完成へと至るだろう。
しかし、ここで数学者は彼の耳の方角の音楽家に降参する。
1760年5月3日 |