反射光学は反射光線に関係した鏡像を取り扱う。
光線が良く磨かれた表面に向かうとき、
それらは四方八方へ角度がそれぞれの間で等しい方法で反射される。
明るい光でこれを評価するためには、
AB（Ｆｉｇ１７）が普通の鏡の表面、
Pが発光点、その光線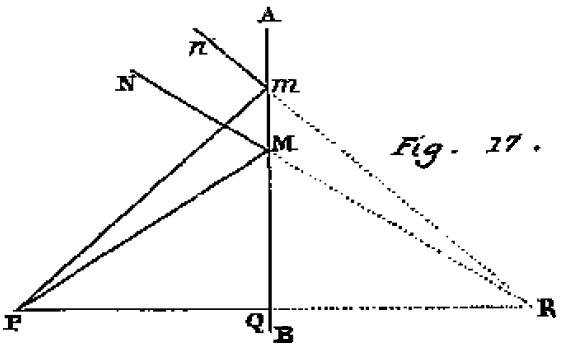
PQ、PM、Pｍが鏡に降り注ぐとしよう。
これらの全光線の内、鏡に垂直に向かい、
さらにこの特別で注目すべき特性をもつ光線をPQとしよう。
即ち、それはQPの方向に自身を反射する。
ちょうどビリヤード台上で、ボールがレッジ（出っ張り）に対して垂直に打たれるとき、
ボールは同じ方向に反発される。
しかし、あらゆる他の光線は、PMのように、
角AMNが角BMPと等しくなるような方法で線MNに反射される。
光線PMは入射光線と呼ばれ、MNは反射光線と呼ばれることに注目すべきである。
同様の方法で、入射光線Pmに対しては反射光線ｍｎが相当するだろう。
その結果、反射のために、光線PMが線MNの方向に続き、
さらに光線Pmがｍｎの方向に続く。
それゆえに、角AMNは角BMPに等しく、角Amnは角BmPに等しい。
この特性は次のように明確に述べられる。反射角は常に入射角に等しい。
私は既にこの注目すべき特性に注意してきた。
しかし、現在のところ、
私の計画はその結果生じる鏡像のこの現象がなんであるかを示すことである。
第一に、Nに置かれた目が発光点Pからの反射光線MNを受けるであろう。
よって、もし対象物Pがちょうどその線のどこかの場所にあったなら、
それが推進される点から物体の感覚を目の中に生じる光線が
MNの方向にやってくる。
ゆえに、目はNMの方向に物体Pを見るはずであるといえる。
より明確にこの事実を明らかにするためには、
われわれは幾何学を頼りにしなければならない。
さらに、あなたは次の理由が発見される命題を、喜んで思い出すだろう。
垂直線PQを鏡の反対側、Rへ延長しよう、
すなわち、QRはPQに等しいはずである。
鏡の裏で延長した全ての反射光線MNとｍｎはその点（R）で出会うはずである
ということを、わたしはあなたに示そう。
つまり、２つの三角形PQMとRQMをとると、それらはまず辺MQを両方に共通にもつ。
そのとき、辺QRは辺PQに等しい。
そして、最後に、直角である角PQMと、その隣接する角RQMは同様に直角でなければならない。
（ユークリッドの原論、書?T．属性１３）
それ故に、２つの等しい辺で挟まれたそれぞれ等しい角を有するこれらの２つの三角形は、
どの点から見ても等しい。（ユークリッドの原論、書?T．属性４）
その結果、角PMQは角RMQに等しい。
しかし、上下関係にある角AMNは角PMQは互いに等しい。
（ユークリッドの原論、書?T．属性１５）
その結果、角AMNもまた角PMQに等しい。
即ち、反射角は入射角に等しいのである。
延長される反射光線ｍｎが同じくR点を通過し、
その結果、異なった辺上ではあるが、
鏡の表面からPと同じ距離で、
この点（R）が垂直面PQR内にあるので、
あたかも物体Pが実際に鏡の裏の点Rに置かれているかのように、
同じ効果を目の中に生じる、
ということが同じ方法で証明される。
これは、それらがその背後にあるかのごとく、なぜ鏡が対象物を写すのか、
そして、なぜわれわれが、これらの対象物が実際その前にあるのと同様に、
鏡の表面のはるか後ろに置かれていると判断するのか、
あなたははっきりと理解することが可能である。
このように、鏡はそれらの外観を変えずに別の場所へ対象物を運ぶということなのである。
鏡の中のその見かけの対象物と実物を区別するため、
われわれは見かけの物体を鏡像と名付け、
さらに、反射光線により描写される鏡像は鏡の背後にある、と言う。
この表明は鏡の中に描写されたそれらの鏡像と実際の対象物を区別するのに役立つ。
さらに、われわれが鏡の中にみる鏡像は、
物体の左にあるものが鏡像では右に、
さらに相反して見えるというこの例外を除いて
全く等しく且つ同一である。
ゆえに、左側に剣を帯びる人は、鏡の中では右にそれをもつように見える。
いままで述べてきた事から、何が鏡の背後にあろうとも、
ある対象物の鏡像を決定することは常に容易である。
と言うのは、鏡をAB（挿絵?T．図１８）、矢である物体をEFとすると、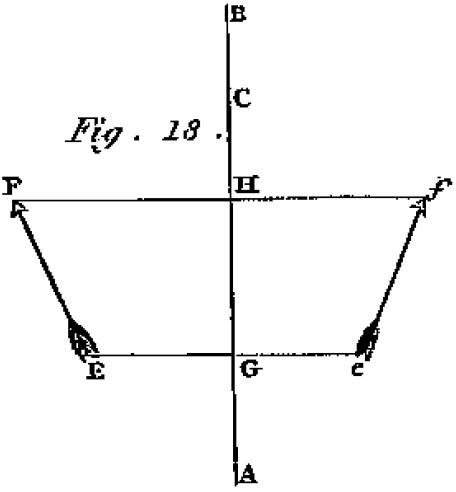
E点とF点から鏡の表面へ垂直線EGとFHを描き、
ｅとｆへこれらを延長する。
ゆえに、ＥＧがｅＧに、ＦＨがｆＨに等しく、
物体ＥＦに等しいｅｆが求められる鏡像である。
なぜなら、四辺形の図ＧｅｆＨは、
全て四辺形の図ＧＥＦＨに等しい。
あなたが鏡であるＣＢやＡＣのような一部分を鏡から切り取ったとしても、
鏡像ｅｆは変えられないであろう、
ということがよりいっそう注目されねばならない。
そして、結果として、鏡が垂直線ＥＧ、ＦＨを降ろせるほど十分に大きくないとき、
われわれがそれらの上に垂直線を降ろそうとするとき、
われわれが幾何学的に線を延長するように、
われわれは鏡の面を拡張しようと想像するはずである。
わたしが述べたことは、表面が完全に平らである普通の鏡のみに関係する。
凸面や凹面鏡は異なった効果を生み出す。
１７６０年８月７日