|
殿下の御前に示すという栄誉をいただいた、さまざまな度合いの速さ(速度)の解明は、音または一般的な雑音の実験へと私を推し進める。
音がわれわれの耳に届く前に、ある一定の時間が常に介在すること、
即ちこの時間は、音が発生したその場所からわれわれまでの距離に応じて長くなる、
ということが認められるはずである。
つまり、音を1142フィート(348.08m)の距離だけ伝達するのに必要な1秒という時間である。
大砲が発射されると、やや離れている者は、
彼らが閃光を見た後、ある時間の間爆音を聴くことは無い。
約5マイル(5×1.609km≒8km)または24000フィート離れた者は、
彼らが閃光を見た後、21秒経過するまで爆音を聞くことは無い。
(訳注:爆音到着までの時間:8km÷348.08m/s≒23秒)
稲光の後、雷の雑音がある時間の間耳に到達しないことを、あなたはおそらく度々気がついているはずである。
そして、これにより、われわれは雷が発生した場所からわれわれの場所までの
距離を計算できるのである。
例えば、もし、閃光と雷のバリバリ言う音の間に20秒の間隔があったと観測したら、
毎秒1142フィート(348.08m/s)の距離を考慮して、
雷の所在地は22、840フィート(22480フィート×0.3048m/フィート≒6.9km)の距離にある
とわれわれは断定できる。
この基本的な特徴は、音を構成するものは何か?という問いにわれわれを導く。
その性質は匂いのそれに似ているのかどうか
−すなわち、われわれの匂いの感覚に影響を与えるよう
計算されたわずかな発散物で空気を満たすことにより
匂いが花から放出されるように、
音がそれを生み出す物体から発せられるのかどうか。
この考えは以前は人を楽しませた。
しかし、鐘を叩くことによりわれわれの耳に伝達されるものは何も無いこと、
また音を生み出す物体はその物質の一部を失うわけではないこと、
が今では証明されている。
われわれが叩かれる鐘または弾かれた楽器の弦を見るとき、
それらの全ての部分が影響を受けることにより、
その時それらの物体が振動または攪拌(激しくゆすぶられている)状態にあることに
われわれは気がつく。
即ち、それらの部分が攪拌されるような影響を受けやすいあらゆる物体がさらに音を生み出す。
それがあまりに小さすぎない場合、これらの揺さぶりまたは振動を楽器の弦に見ることができる。
ピンと張った弦ACBはAMBとANBの状態を交互に通過する。
(Fig.1を見よ。私がこれらの振動を、それらが実際に振動するよりも感覚的により一層わかりやすく表現した。)

これらの振動が、われわれの聴覚器官を叩くため
ようやくたどり着くまでに
空気のさらに離れた部分へ
うまく伝達させるのと同じ振動で、
隣接する空気を押すことが観察されるはずである。
さらにこれらの振動を受け、且つわれわれの耳まで音を送出するのが空気である。
それ故に、音の知覚力は、聴覚器官を通してわれわれに伝達される空気の振動により
われわれの耳に作用する効果であるという意外の何ものでも無い、
ということは明らかである。
そして、われわれは弾かれた弦の音を聞くとき、
われわれの耳は弦が同時に振動を起こすのと同様の多くの打音を空気から受ける。
かくして、もし弦が1秒間に100の振動を起こすならば、
同様に、耳は同時に100の打音を受ける。
そして、これらの打音の知覚が、われわれが音と呼ぶものなのである。
これらの打音が互いに一様にうまくいくとき、
またはこれらの間隔が全て等しいとき、
音は均整のとれたものになり、いわば音楽の必要条件となるのである。
.しかし、打音が不均等になるか、またはそれらの間隔が自身の間で不均等になると、
その結果、音楽では不規則な雑音、互いに相いれないものとなる。
振動が均一に発生する音楽の音を多少でももっと注意深く考慮してみると、
私は最初に、耳に影響を与えた打音と同様に、振動は強さの多少であり、
音の相違はそれを原因とするのではなく、
音楽家によりフォルテピアノと呼ばれる特性を生み出す強弱による、
ということに気が付く。
しかし、振動が多少急速な場合、即ち、それらの増減が1秒間に行われるとき、
そこにはより一層異なった本質がある。
1本の弦が1秒間に100回振動し、同時に別の弦が1秒間に200回振動するとき、
それらの音は本質的に異なるのである。
前者はより低いかフラット(♭)であり、他方はより高いかシャープ(♯)である。
全ての音楽は蝶番のようにつながり、
平坦さや荒々しさの点で異なった音を結合する方法の一方で、
心地よい和声(和音)を生み出すことと同様の方法を教えてくれる、
そのようなフラット(♭)とシャープ(♯)音の間には真の相違がある。
フラット(♭)音は、シャープ(♯)音よりも同時刻における振動は少ない。
そして、ハープシコードの全ての鍵盤は1秒間に収まるある一定の決まった振動数を含む。
このように、文字Cにより記される音は1秒間に約100回振動し、
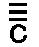 で記される音は同じ時間間隔に1600回振動する。 で記される音は同じ時間間隔に1600回振動する。
1秒間に100回振動する弦は正確に音Cを出す。
そしてもし50回だけ振動するならば、音はより低いかよりフラット(♭)になるだろう。
しかしわれわれの耳に関しては、これ以上知覚できないという音のある限界がある。
われわれは、1秒間に30回以下の振動を起こす弦の音も、音が余りに低すぎるので、
さらに1秒間に7552回以上の振動を起こす弦の音も、音が余りに高すぎるので、
どちらも判断することができないようである。
1760年4月26日
|