|
3.M.マスカート氏の解説
ランジュバンの論文は見出し無しの3部に分けられる。
かれのブラウン運動の分析は、“そして、更にその上、・・・の証明を与えるのは容易である”の字句と共にパートⅡの最初の文で始まり、そして、パートⅡの終わりへと続く。
この分析は、自己完結しており、彼の論文の大部分を構成し、今日の物理学者にもっとも興味あるものだろう。
しかしながら、注意深い読者は、パートⅠとⅢの出典に関するランジュバンの特性評価が問題を含むことに気付くだろう。
ブラウン粒子の変位を意味する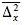 の正しい形式と量的な検証については未 の正しい形式と量的な検証については未
解決である。
パートⅠでは、ランジュバンは、ランジュバンの方程式(1)で報告される
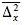 の関数形式を引き出す後半で、アインシュタインの2つの論文を参照して
の関数形式を引き出す後半で、アインシュタインの2つの論文を参照して
いる。
パートⅡでは、ランジュバン自身の解析が方程式(1)を再び生みだす。
これは非常に明確である。
一方、スモルコフスキーは、“(1)と同じ形式の表現の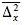 を得ている を得ている
が、係数64/17の点でそれとは異なった”別の理論を使用している。スモルコフスキーの理論は、アインシュタイン/ランジュバンの式(1)で予言されるものより、係数64/27より大きいかまたは係数27/64より小さい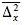 の値を予言するのだろうか?
の値を予言するのだろうか?
もしこの翻訳にここでわずかに曖昧さがあるとしても、ランジュバンのフランスでも同様の曖昧性が反映されるにすぎない。
自然に読めば、スモルコフスキーの予言はアインシュタインとランジュバンの係数64/27よりも大きいのである。
スモルコフスキーの論文の精査はこの説明を確認するものである。われわれは、問題を引き出すためにこの詳細を簡単に述べる。
パートⅢでは、われわれは、スベドベリのそれらと、明らかにこれら、“式(1)で与えられるこれらと凡そ1:4の比だけ異なる”
理論を比較することで、ランジュバンを有効にする実験結果のみを見出す。
繰り返すが、自然な説明は、スベドベリの測定がアインシュタイン/ランジュバンの式(1)によって予言された大きさの1/4の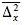 の値と一致するこ の値と一致するこ
とである。
理論と実験の間のそのような相違は、おそらく新たな分野においては例外ではない。しかしながら、ランジュバンは、スベドベリの実験結果は、文の後半から引用すると“M.スモルコフスキーの式で計算したそれに近い”と言い続ける。これをどうすべきか?
スモルコフスキーは、スベドベリがアインシュタイン/ランジュバンの式(1)のそれより小さい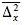 を測定するかぎり、二乗変位 を測定するかぎり、二乗変位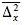 は、大きいと は、大きいと
予言する。
だが、スベドベリの結果は、スモルコフスキーにより予言されたそれらにより近いと思われる!
明らかにランジュバンはこのケースを誤って述べている。
如何なる方法なのか、如何なる理由なのか、まったくわれわれにはわからない。
もし、われわれがランジュバンの解説のあら捜しをしなければならないとしたら、われわれは彼の物理学を賞賛することになる。
そもそも、ランジュバンは、たとえスモルコフスキーの理論が健全であろうとも、それに関するかれの計算結果は誤っている、ということを発見した。ランジュバンはスモルコフスキーの計算の誤りを正し、疑わしい係数64/27無しでも式(1)を引き出せることを見出した。
ランジュバンはまた、スベドベリの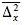 の測定が直接でないこと、及び後 の測定が直接でないこと、及び後
半で、観測されたブラウン粒子はおそらく小さすぎて、式(1)が依存するストークスの方程式を呼び出すしかないことをはっきりと認めた。
幸いにも、ランジュバンは、創られた無効な理論と無効な実験の収斂よりも、彼とアインシュタインのよく動機付けされ、よく履行された理論に信頼を置いていた。
|