|
われわれがこれまで考えてきた上に、
オクターブの進行を含む1:2、1:4、1:8、1:16の関係は、
数字2のみにより形成される。
というのは、4は2の2倍、8は2の4倍、16は2の8倍であるからである。
それゆえに、われわれが音楽に数字2だけを認めるならば、
われわれは、音楽家が1、2、3オクターブと呼ぶ和音
またはコンソナンス(協和音)だけの知識に達するはずなのだ。
さらに数字2は倍加することにより数字4,8,16,32,64のみを与えるが、
ここでは常に前にある値を2倍し、(64以降の)他の数は未知のままとする。
さて、音がC,c、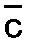 、 、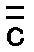 、 、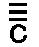 と印されるように、 と印されるように、
楽器がオクターブのみを含み、さらにその他全ての音が除外されたなら、
あまりに単純化され過ぎて心地よい音楽は生まれることができない。
次に、数字2、数字3を共に紹介しよう。
そして和音またはコンソナンス(協和音)の結果何が起きるのか観察してみよう。
1:3の比はすぐに2つの音を表わし、一方は同時に他方よりも3倍多く振動する。
この比はおそらく1:2の比の次に最も容易に理解できる。
従って、それはオクターブの比とは全く異なった性質の、
非常に心地よいコンソナンス(協和音)を提供するだろう。
次に、数字1が音Cに一致する1:3の比でのそれを仮定してみよう。
音cは数字2によって表現されるので、
数字3はcより高い音を与えるが、
同時に数字4に一致する音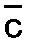 よりも低い。 よりも低い。
さて、数字3で表現される音は
音楽家が文字gを付ける音であり、
かれらはcからgの間隔を5度と呼ぶ、
なぜなら、ハープシコードの鍵盤で、
gの音はc,d,e,f,gのようにcから5番目であるからだ。
そのとき、もし数字1が音Cを発生するなら、数字2はcを、数字3はgを、
数字4は音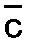 を与えるだろう。 を与えるだろう。
音gのオクターブ上の音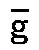 は、それに一致する数字2の3倍または6だろう。 は、それに一致する数字2の3倍または6だろう。
さらに1オクターブ上がると、音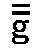 は2倍大きい数、即ち12に一致するだろう。 は2倍大きい数、即ち12に一致するだろう。
それ故に、2つの数字2と3がわれわれに示す全ての音は、音Cを1で示すと、
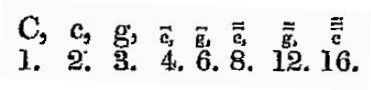
となる。
故に、1オクターブと5度を混合した1:3の比が間隔を表わすことは明らかである。
そして、それを表現する数の単純さのために、
この間隔はオクターブに続いて耳にもっとも心地良いのである。
したがって、音楽家は第五までのコンソナンス(協和音)間に第二を配置する。
そして、聴覚はそれを非常に容易に捕らえるので、第五を調音するのに困難は無い。
この理由により、バイオリンでは、4本の弦が5度、
つまり最も低いg、第二が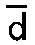 、第三が 、第三が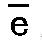 、第四が 、第四が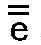 までの音を発生する。* までの音を発生する。*
そしてあらゆる音楽家が聴覚だけでそれらを調律する。
しかしながら、5度は1オクターブのように容易に調音できない。
1:3の比により表現されるCからgのようにオクターブを超える5度は、
2:3の比で表現されるCからGまたはcからgのように単純な5度よりも知覚可能である。
そして、音Cに固定することで、
同様に単純なGよりもより高い5番目のgに調律することが容易であることは
実験により知られている。
もし1が音Fに印されると、数字3は音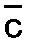 を示す。 を示す。
そのために
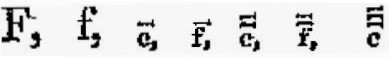 は は
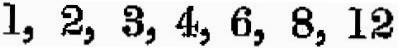 と示され、fからcの間隔は2:3の関係で第五となる。 と示され、fからcの間隔は2:3の関係で第五となる。
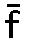 から から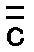 、 、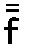 から から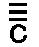 もまた4:6、8:12の比と同様2:3の比と同じである。 もまた4:6、8:12の比と同様2:3の比と同じである。
というのは、もし2つの弦が同時に1つが4振動、もう一つが6振動を行ったなら、
前者の弦は最初の時間間隔の半分に等しい時間で2つの振動を起こすだろう。
第二は、同時に3つの振動を起こすだろう。
次に、これらの弦から発せられる音は2つの場合同じである。
4:6の関係の結果は2:3のそれと同じ間隔を表わす。即ち第5である。
その結果、われわれは、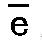 と と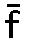 の比であり、 の比であり、
結果としてcとf、CとFの比でもである3:4の比を含んだ別の間隔の知識に到達した。
音楽家はそれを4度と呼ぶ。
そして、より大きな数によって表現されると、
多すぎて、それは5度のようにあまり心地よくなく、
オクターブよりもさらに少ない。
数字3は新しい和音またはコンソナンス(協和音)、即ち5度と4度を示すので、
われわれが他の名前で呼ぶ前に、
音3または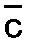 (1オクターブおよび5度)より高い音を与える数字9を手にするために、 (1オクターブおよび5度)より高い音を与える数字9を手にするために、
それを再度3倍しよう。
さて、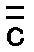 は は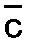 の1オクターブ上であり、 の1オクターブ上であり、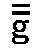 は は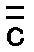 から5度である。 から5度である。
そのとき、数字9は音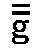 を与える。そのため、 を与える。そのため、
 は、 は、
 と印されるだろう。 と印されるだろう。
そして、もしこれらの音が低いオクターブで取られるならば、
関係はそのまま同じで、新たな間隔の知識へとわれわれを導くのである。

第一は、音楽家が2度または全音と呼ぶ8:9の比を含んだF:Gの比である。
第二は、7度と呼ばれる9:16の比を含んだG:fの比であり、
さらにそれは1オクターブ以下の2度または全音である。
既に非常に大きな数で表現されるこれらの比は、コンソナンス(協和音)間を数えられない。
また音楽家はそれらをディソナンスまたはディスコード(不協和音)と呼ぶ。
繰り返すが、もしわれわれが数字9を3倍すると27となり、
それは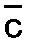 よりも高い音程を示し、正確にはgよりも5度高い。 よりも高い音程を示し、正確にはgよりも5度高い。
従って、それは音程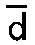 であり、 であり、
その1オクターブ上の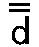 は数字27の2倍、54と一致し、 は数字27の2倍、54と一致し、
さらにその2倍オクターブ上の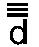 は数字54の2倍、108と一致する。 は数字54の2倍、108と一致する。
次の方法でこれらの音を低いほうのいくつかのオクターブで表わしてみよう。
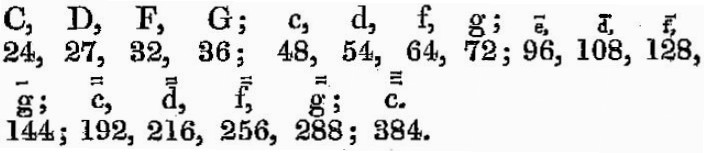
故に、われわれは、DからFの間隔が27:32の比に等しく、
F:dの間隔が32:54の比に等しく、
2で割り切れる2つの数であるということを知る。
さらに、この関係から、われわれは16:27の比を知るのである。
最初の間隔はtierce minor(ティアスマイナー:3度短音程)、
またはlesser third(3度以下)と呼ばれ、
他はさらにgreater sixth(6度以上)と呼ばれる。
数27はさらに3倍されたものでなけれならない。
しかし、音楽は限りなく広がることはなく、
そしてわれわれは3そのものを3度掛けた3の結果としての数字27までに制限する。
さらに望みの他の音楽の音は数5により始まり、次の私の手紙で説明されるだろう。
1760年5月3日
(編注:* 即ち、音節の一式(ド、レ・・・シ)を借りていえば、ソ、レ、ラ、ミである。) |